希望学校八年级共有4个班，在世界地球日来临之际，每班各选拔10名学生参加环境知识竞赛，评出了一、二、三等奖各若干名，校学生会将获奖情况绘制成如图所示的两幅不完整的统计图，请依据图中信息解答下列问题：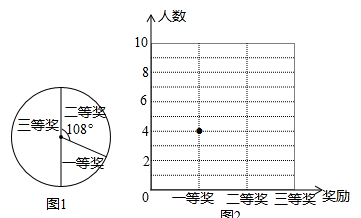
（1）本次竞赛获奖总人数为 人；获奖率为 ；
（2）补全折线统计图；
（3）已知获得一等奖的4人为每班各一人，学校采取随机抽签的方式在4人中选派2人参加上级团委组织的“爱护环境、保护地球”夏令营，请用列举法求出抽到的两人恰好来自二、三班的概率．
已知二次函数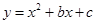
中，函数
与自变量
的部分对应值如下表：
|
… |
 |
 |
 |
 |
 |
 |
… |
|
… |
 |
 |
|
|
|
|
… |
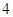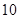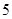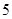（1）求该二次函数的关系式；
（2）当为何值时，有最小值，最小值是多少？
（3）若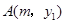
，
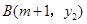两点都在该函数的图象上，试比较
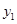与
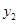的大小．
已知：o为坐标原点，∠ AOB=300 , ∠ABO=900且A(2,0)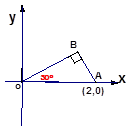
求:过A、B、O三点的二次函数解析式
已知如图，二次函数y=ax2 +bx+c的图像过A、B、C三点
(1)观察图像写出A、B、C三点的坐标
(2)求出二次函数的解析式
已知二次函数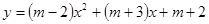
的图象过点（0， 5）
⑴ 求m的值，并写出二次函数的关系式；
⑵ 求出二次函数图象的顶点坐标、对称轴．
已知二次函数y=-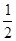
x2 –x+4回答下列问题
（1）用配方法将其化成y="a" (x-h)2+k的形式
（2）指出抛物线的顶点坐标和对称轴
（3）当x取何值时，y随x增大而增大; 当x取何值时，y随x增大而减小？