如图,正方体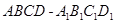 的棱长为2,E,F,G分别是
的棱长为2,E,F,G分别是 ,
, 的中点.
的中点.
(1)求证:FG//平面 ;
;
(2)求FG与平面 所成的角的正切值.
所成的角的正切值.
(12分)已知 有两个不等的负根,
有两个不等的负根, 无实数根,若p或q为真,p且q为假,求m的取值范围。
无实数根,若p或q为真,p且q为假,求m的取值范围。
已知圆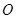 的方程为
的方程为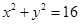 ,过点
,过点 作直线与圆
作直线与圆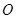 交于
交于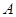 、
、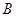 两点。
两点。
(1)若坐标原点O到直线AB的距离为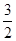 ,求直线AB的方程;
,求直线AB的方程;
(2)当△ 的面积最大时,求直线AB的斜率;
的面积最大时,求直线AB的斜率;
(3)如图所示过点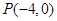 作两条直线与圆O分别交于R、S,若
作两条直线与圆O分别交于R、S,若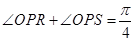 ,且两角均为正角,试问直线RS的斜率是否为定值,并说明理由。
,且两角均为正角,试问直线RS的斜率是否为定值,并说明理由。
如图,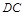 ⊥平面
⊥平面 ,
, =90°,
=90°, ,点
,点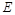 在
在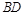 上,点E在BC上的射影为F,且
上,点E在BC上的射影为F,且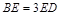 .
.
(1)求证: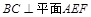 ;
;
(2)若二面角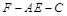 的大小为45°,求
的大小为45°,求 的值.
的值.
如图,在四棱锥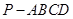 中,底面ABCD是一直角梯形,
中,底面ABCD是一直角梯形,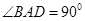 ,
, ,
,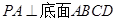 ,且PA=AD=DC=
,且PA=AD=DC=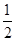 AB=1.
AB=1.
(1)证明:平面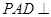 平面
平面
(2)设AB,PA,BC的中点依次为M、N、T,求证:PB∥平面MNT
(3)求异面直线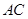 与
与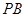 所成角的余弦值
所成角的余弦值
已知点 、
、 到直线
到直线 的距离相等,且直线
的距离相等,且直线 经过两条直线
经过两条直线 和
和 的交点,求直线
的交点,求直线 的方程。
的方程。