如图，抛物线y=ax2+bx（a＞0）经过原点O和点A（2，0）．
（1）写出抛物线的对称轴与x轴的交点坐标；
（2）点（x1，y1），（x2，y2）在抛物线上，若x1＜x2＜1，比较y1，y2的大小；
（3）点B（-1，2）在该抛物线上，点C与点B关于抛物线的对称轴对称，求直线AC的函数关系式．
某厂生产A，B两种产品．其单价随市场变化而做相应调整．营销人员根据前三次单价变化的情况，绘制了如下统计表及不完整的折线图：
A，B产品单价变化统计表
| 第一次 |
第二次 |
第三次 |
|
| A产品单价（元/件） |
6 |
52 |
63．5 |
| B产品单价（元/件） |
3．5 |
4 |
3 |
并求得A产品三次单价的平均数和方差：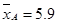
：
．
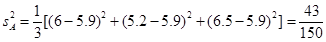（1）补全图中B产品单价变化的折线图．B产品第三次的单价比上一次的单价降低了____%；
（2）求B产品三次单价的方差，并比较哪种产品的单价波动小：
（3）该厂决定第四次调价，A产品的单价仍为6．5元/件，B产品的单价比3元/件上调m%（m＞0），使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1．求m的值．
水平放置的容器内原有210毫米高的水，如图．将若干个球逐一放入容器中，每放入一个大球水面就上升4毫米，每放入一个小球水面就上升3毫米，假定放入容器中的所有球完全浸没水中且水不溢出，设水面高为y毫米．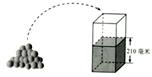
（1）只放入大球，且个数为x大，求y与x大的函数关系式（不必写出x大的范围）；
（2）仅放入6个大球后，开始放入小球，且小球个数为x小．
①求y与x小的函数关系式（不必写出x小的范围）；
②限定水面高不超过260毫米，最多放入几个小球？
嘉淇同学要证明命“两相对边分别相等的四边形是平行四边形”是正确的，她先用尺规作出了如图的四边形ABCD，并写出了如下不完整的已知和求证．
已知：如图，在四边形ABCD中，
BC＝AD，
AB＝____．
求证：四边形ABCD是____四过形．
（1）在方框中填空，以补全已知和求证；
（2）按嘉淇的想法写出证明：
证明：
（3）用文宇叙述所证命题的逆命题为____________________．
老师在黑板上写了一个正确的演算过程，随后用手掌捂住了一个二次三项式，形式如下：
－3x＝x2－5x＋1．
（1）求所捂的二次三项式：
（2）若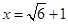
，求所捂二次三项式的值．
如图，在平面直角坐标系中，平行四边形
如图放置，将此平行四边形绕点O顺时针旋转90°得到平行四边形
．抛物线
经过点A、C、A′三点．
（1）求A、A′、C三点的坐标；
（2）求平行四边形和平行四边形重叠部分
的面积；
（3）点M是第一象限内抛物线上的一动点，问点M在何处时，
的面积最大？最大面积是多少？并写出此时M的坐标．