如图,方格纸中的每个小正方形边长都是1个长度单位,Rt△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(1,1),点B的坐标为(4,1).
(1)先将Rt△ABC向左平移5个单位长度,再向下平移1个单位长度得到Rt△A1B1C1,试在图中画出Rt△A1B1C1,并写出点A1的坐标;
(2)再将Rt△A1B1C1绕点A1顺时针旋转90°后得到Rt△A2B2C2,试在图中画出Rt△A2B2C2,并计算Rt△A1B1C1在上述旋转过程中点C1所经过的路径长.
(本小题满分7分)解不等式组 ,并
,并
把它的解集在数轴上表示出 来.
来.
如图,在平面直角坐标系中,抛物线y=x2+mx+n经过点A(3,0)、
B(0, -3),点P是直线AB上的动点,过点P作x轴的垂线
-3),点P是直线AB上的动点,过点P作x轴的垂线 交抛物线于点M,设点P的横
交抛物线于点M,设点P的横
坐标为t.
(1)分别求出直线AB和这条抛物线的解析式.
(2)若点P在第四象 限,连接AM、BM,当线段PM最长时,求△ABM的面积.
限,连接AM、BM,当线段PM最长时,求△ABM的面积.
(3)是否存在这样的点P,使得以点P、M、B、O为顶点的四边形为平行四边形?若存在,请直接写出点P的横坐标;若不存在,请说明理由.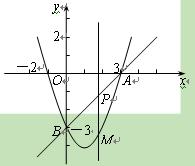
如图,已知CD是⊙O的直径,AC⊥CD,垂足为C,弦DE∥OA,直线AE、CD
相交于点B.
(1)求证:直线AB是⊙O的切线.
(2)当AC=1,BE=2,求tan∠OAC的值.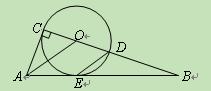
南宁市五象新区有长24000m的新建道路要铺上沥青.
(1)写出铺路所需时间t(天)与铺路速度v(m/天)的函数关系式.
(2)负责铺路的工程公司现有的铺路机每天最多能铺路400m,预计最快多少天可以完成铺路任务?
(3)为加快工程进度,公司决定投入不超过400万元的资金,购进10台更先进的铺路机.现有甲、乙两种机器可供选择,其中每种机器的价格和日铺路能力如下表.在原有的铺路机连续铺路40天后,新购进的10台机器加入铺路,公司要求至少比原来预计的时间提前10天完成任务.问有哪几种方案?请你通过计算说明选择哪种方案所用资金最少.
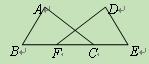
如图,点B、F、C、E在同一直线上,并且BF=CE,∠B=∠C.
(1)请你只添加一 个条件(不再加辅助线),使得△ABC≌△DEF.你添加的条件是:.
个条件(不再加辅助线),使得△ABC≌△DEF.你添加的条件是:.
(2)添加了条件后,证明△ABC≌△DEF.