（本小题满分14分）围建一个面积为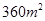
的矩形场地，要求矩形场地的一面利用旧墙（利用的旧墙需维修，可供利用的旧墙足够长），其他三面围墙要新建，在旧墙对面的新墙上要留一个宽
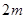的进出口，如图2所示．已知旧墙的维修费用为
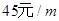，新墙的造价为
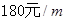．设利用旧墙的长度为
（单位：
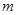），修建此矩形场地围墙的总费用为
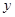（单位：元）．
（1）将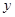表示为的函数，并写出此函数的定义域；
（2）若要求用于维修旧墙的费用不得超过修建此矩形场地围墙的总费用的15%，试确定，使修建此矩形场地围墙的总费用最小，并求出最小总费用．
平面上有9个点,其中有4个点在同一条直线上,此外任三点不共线.
(1)过每两点连线,可得几条直线?
(2)以每三点为顶点作三角形,可作几个?
(3)以一点为端点,作过另一点的射线,这样的射线可作出几条?
某次足球赛共12支球队参加，分三个阶段进行：
（1）小组赛：经抽签分成甲、乙两组，每组6队进行单循环比赛，以积分及净剩球数取前两名；
（2）半决赛：甲组第一名与乙组第二名，乙组第一名与甲组第二名作主客场交叉淘汰赛（每两队主客场各赛一场）决出胜者;
(3)决赛：两个胜队参加决赛一场，决出胜负.
问全部赛程共需比赛多少场？
平面α内有5个点，平面β内有4个点，用其中4个点作一四面体的4个顶点，最多可构成多少个四面体？
4位同学参加某种形式的竞赛，竞赛规则：每位同学必须从甲、乙两道题中任选一题作答，选甲题答对得100分，答错得—100分；选乙题答对得90分，答错得—90分.若4位同学的总分为0，则这4位同学有多少种不同的得分情况？
现有6本不同的书，如果（1）分成三组，一组3本，一组2本，一组1本；
（2）分给三个人，一人3本，一人2本，一人1本；
（3）平均分成三个组.
分别求分法种数.