(本题14分)设圆满足:(1)截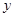 轴所得弦长为2;(2)被
轴所得弦长为2;(2)被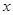 轴分成两段弧,其弧长的比为
轴分成两段弧,其弧长的比为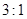 ,在满足条件(1)(2)的所有圆中,求圆心到直线
,在满足条件(1)(2)的所有圆中,求圆心到直线 的距离最小的圆的方程.
的距离最小的圆的方程.
已知椭圆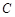 的方程为
的方程为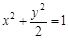 ,点
,点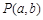 的坐标满足
的坐标满足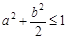 过点
过点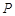 的直线
的直线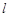 与椭圆交于
与椭圆交于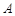 、
、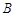 两点,点
两点,点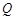 为线段
为线段 的中点,求:
的中点,求:
(1)点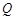 的轨迹方程;
的轨迹方程;
(2)点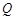 的轨迹与坐标轴的交点的个数.
的轨迹与坐标轴的交点的个数.
设f(x)是定义在区间 上以2为周期的函数,对
上以2为周期的函数,对 ,用
,用 表示区间
表示区间 已知当
已知当 时,f(x)=x2.
时,f(x)=x2.
(1)求f(x)在 上的解析表达式;
上的解析表达式;
(2)对自然数k,求集合 不等的实根}
不等的实根}
设函数 ,其中
,其中 .
.
(1)解不等式 ;
;
(2)求 的取值范围,使函数
的取值范围,使函数 在区间
在区间 上是单调函数.
上是单调函数.
(本小题满分14分)已知函数 ,
, ,其中
,其中 ,
, 为自然对数的底数.
为自然对数的底数.
(Ⅰ)当 时,求函数
时,求函数 的极小值;
的极小值;
(Ⅱ)对 ,是否存在
,是否存在 ,使得
,使得 成立?若存在,求出
成立?若存在,求出 的取值范围;若不存在,请说明理由;
的取值范围;若不存在,请说明理由;
(Ⅲ)设 ,当
,当 时,若函数
时,若函数 存在
存在 三个零点,且
三个零点,且 ,求证:
,求证:  .
.
(本小题满分13分)已知椭圆 :
: (
( )的右焦点为
)的右焦点为 ,且过点
,且过点 .
.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)设直线 与椭圆
与椭圆 交于不同两点
交于不同两点 、
、 ,且
,且 .若点
.若点 满足
满足 ,求
,求 的值.
的值.