如图,圆周角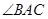 的平分线与圆交于点
的平分线与圆交于点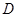 ,过点
,过点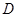 的切线与弦
的切线与弦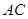 的延长线交于点
的延长线交于点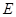 ,
, 交
交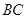 于点
于点 .
.
(1)求证: ;
;
(2)若 四点共圆,且弧
四点共圆,且弧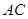 与弧
与弧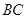 相等,求
相等,求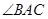 .
.
如图,某动物园要建造两间完全相同的矩形熊猫居室,其总面积为24平方米,设熊猫居室的一面墙AD的长为x米  .
.
(1)用x表示墙AB的长;
(2)假设所建熊猫居室的墙壁造价(在墙壁高度一定的前提下)为每米1000元,请将墙壁的总造价y(元)表示为x(米)的函数;
(3)当x为何值时,墙壁的总造价最低?
如图,在四棱锥P-ABCD中,底面ABCD是正方形,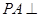 底面
底面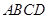 ,且PA=AB.
,且PA=AB.
(1)求证:BD 平面PAC;
平面PAC;
(2)求异面直线BC与PD所成的角.
某市为节约用水,计划在本市试行居民生活用水定额管理,为了较为合理地确定居民日常用水量的标准,通过抽样获得了100位居民某年的月均用水量(单位:吨),右表是100位居民月均用水量的频率分布表,根据右表解答下列问题:
| 分组 |
频数 |
频率 |
| [0,1) |
10 |
0.10 |
| [1,2) |
 |
0.20 |
| [2,3) |
30 |
0.30 |
| [3,4) |
20 |
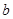 |
| [4,5) |
10 |
0.10 |
| [5,6] |
10 |
0.10 |
| 合计 |
100 |
1.00 |
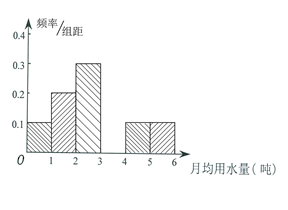
(1)求右表中 和
和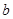 的值;
的值;
(2)请将频率分布直方图补充完整,并根据直方图估计该市每位居民月均用水量的众数.
已知函数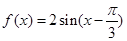 ,
, .
.
(1)写出函数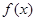 的周期;
的周期;
(2)将函数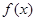 图象上的所有的点向左平行移动
图象上的所有的点向左平行移动 个单位,得到函数
个单位,得到函数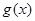 的图象,写出函数
的图象,写出函数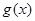 的表达式,并判断函数
的表达式,并判断函数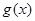 的奇偶性.
的奇偶性.
已知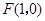 ,直线
,直线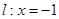 ,
,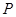 为平面上的动点,过点
为平面上的动点,过点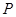 作
作 的垂线,垂足为点
的垂线,垂足为点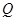 ,且
,且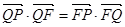 .
.
(1)求动点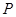 的轨迹曲线
的轨迹曲线 的方程;
的方程;
(2)设动直线 与曲线
与曲线 相切于点
相切于点 ,且与直线
,且与直线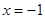 相交于点
相交于点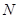 ,试探究:在坐标平面内是否存在一个定点
,试探究:在坐标平面内是否存在一个定点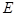 ,使得以
,使得以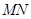 为直径的圆恒过此定点
为直径的圆恒过此定点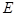 ?若存在,求出定点
?若存在,求出定点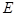 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.