(本小题满分12分)为了研究某种细菌随时间x变化,繁殖的个数,收集数据如下:

(1)用天数作解释变量,繁殖个数作预报变量,作出这些数据的散点图,根据散点图判断: 与y=
与y=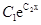 哪一个作为繁殖的个数y关于时间x变化的回归方程类型为最佳?(给出判断即可,不必说明理由)
哪一个作为繁殖的个数y关于时间x变化的回归方程类型为最佳?(给出判断即可,不必说明理由)

其中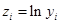 ;
;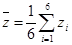
(2)根据(1)的判断最佳结果及表中的数据,建立y关于x 的回归方程。
参考公式: 

如图,已知四棱锥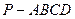 中,底面
中,底面 是直角梯形,
是直角梯形, ,
,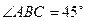 ,
,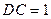 ,
,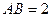 ,
, 平面
平面 ,
, .
.
(1)求证: 平面
平面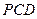 ;
;
(2)求证: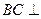 平面
平面 ;
;
(3)若M是PC的中点,求三棱锥M—ACD的体积.
已知函数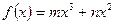 (
( )在
)在 时有极值,其图象在点
时有极值,其图象在点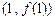 处的切线与直线
处的切线与直线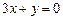 平行。
平行。
(1)求m,n的值; (2)求函数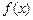 的单调区间。
的单调区间。
某工厂有A、B两种配件生产甲、乙两种产品,每生产一件甲产品使用4个A配件耗时1h,每生产一件乙产品使用4个B配件耗时2h,该厂每天最多可从配件厂获得16个A配件和12个B配件,按每天8h计算,若生产一件甲产品获利2万元,生产一件乙产品获利3万元,采用哪种生产安排利润最大?
在△ABC中,已知B=45°,D是BC边上的一点,AB=5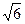 ,AC="14," DC=6,求AD的长.
,AC="14," DC=6,求AD的长.
已知函数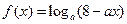
(1)若 ,求实数
,求实数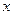 的取值范围;
的取值范围;
(2)若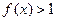 在区间[1,2]上恒成立,求实数
在区间[1,2]上恒成立,求实数 的取值范围.
的取值范围.