(本小题满分12分) 学生的学习能力参数 可有效衡量学生的综合能力,
可有效衡量学生的综合能力, 越大,综合能力越强,为推动数学知识的发展,提高学生的综合能力。某校根据学生的学习能力参数
越大,综合能力越强,为推动数学知识的发展,提高学生的综合能力。某校根据学生的学习能力参数 将参加数学竞赛小组的学生分成了如下三类:
将参加数学竞赛小组的学生分成了如下三类:
学习能力参数 |
学习能力参数 |
||
 |
 |
 |
|
| 学生人数(人) |
15 |
10 |
 |
某研究性学习小组,从该竞赛小组中按分层抽样的方法随机选取了 人,根据其学习能力参数
人,根据其学习能力参数 ,作出了频率与频数的统计表:
,作出了频率与频数的统计表:
| 分组 |
频数(人) |
频率 |
 |
3 |
|
 |
 |
 |
 |
|
 |
| 合计 |
 |
 |
(1)求 ,
, ,
, ,
, 的值
的值
(2)规定:学习能力参数 不少于70称为优秀。若从这
不少于70称为优秀。若从这 人中任选
人中任选 人,记抽到到的优秀人数为随机变量
人,记抽到到的优秀人数为随机变量 ,求
,求 的分布列和数学期望
的分布列和数学期望
已知 是函数
是函数 的一个极值点.
的一个极值点.
(Ⅰ)求实数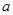 的值;
的值;
(Ⅱ)求函数 的单调区间.
的单调区间.
已知函数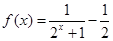 .
.
(Ⅰ)若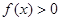 ,求实数
,求实数 的取值范围;
的取值范围;
(Ⅱ)判断函数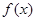 的奇偶性,并说明理由.
的奇偶性,并说明理由.
记函数 的定义域为集合
的定义域为集合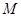 ,函数
,函数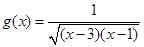 的定义域为集合
的定义域为集合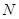 .求:
.求:
(Ⅰ)集合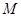 ,
,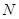 ;
;
(Ⅱ)集合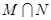 ,
,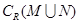 .
.
假设你家订了一份报纸,送报人可能在早上6点—8点之间把报纸送到你家,你每天离家去工作的时间在早上7点—9点之间
(1)你离家前不能看到报纸(称事件A)的概率是多少?(6分,须有过程)
(2)请你设计一种随机模拟的方法近似计算事件A的概率(包括手工的方法或用计算器、计算机的方法)
(本小题满分12分)在人群流量较大的街道,有一中年人吆喝“送钱”,只见他手拿一黑色小布袋,袋中有3只黄色、3只白色的乒乓球(其体积、质地完成相同),旁边立着一块小黑板写道:
摸球方法:从袋中随机摸出3个球,若摸得同一颜色的3个球,摊主送给摸球者5元钱;若摸得非同一颜色的3个球,摸球者付给摊主1元钱。
(1)摸出的3个球为白球的概率是多少?
(2)摸出的3个球为2个黄球1个白球的概率是多少?
(3)假定一天中有100人次摸奖,试从概率的角度估算一下这个摊主一个月(按30天计)能赚多少钱?