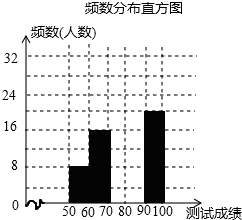
苏州某中学为了迎接第53届世乒赛，在九年级举行了“乒乓球知识竞赛”，从全年级600名学生的成绩中随机抽选了100名学生的成绩，根据测试成绩绘制成以下不完整的频数分布表和频数分布直方图：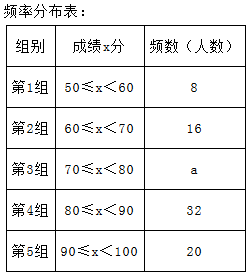
请结合图表完成下列各题：
（1）求表中a的值：
（2）请把频数分布直方图补充完整
（3）若测试成绩不低于90分的同学可以获得第53届世乒赛吉祥物“乒宝”，请你估计该校九年级有多少位同学可以获得“乒宝”?
已知，如图，AB∥ED，点F、点C在AD上，AB=DE,AF=DC.
求证：BC="EF."
先化简，再求值：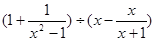
，其中
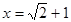
解方程：
.
（本小题满分8分）如图，在平面直角坐标系中，点O是坐标原点，四边形AOCB是梯形，AB∥OC，点A在y轴上，点C在x轴上，且
，OB＝OC．
（1）求点B的坐标；
（2）点P从C点出发，沿线段CO以5个单位/秒的速度向终点O匀速运动，过点P作PH⊥OB，垂足为H，设△HBP的面积为S（S≠0），点P的运动时间为t秒，求S与t之间的函数关系式（直接写出自变量t的取值范围）；
（3）在（2）的条件下，过点P作PM∥CB交线段AB于点M，过点M作MR⊥OC，垂足为R，线段MR分别交直线PH、OB于点E、G，点F为线段PM的中点，联结EF．
①判断EF与PM的位置关系；
②当t为何值时，
？
（本小题满分7分）如图，已知二次函数
的图象与x轴负半轴交于点A（-1，0），与y轴正半轴交与点B，顶点为P，且OB=3OA，一次函数y=kx+b的图象经过A、B．
（1）求一次函数解析式；
（2）求顶点P的坐标；
（3）平移直线AB使其过点P，如果点Ｍ在平移后的直线上，且
，求点M坐标；
（４）设抛物线的对称轴交x轴与点E，联结AP交y轴与点D，若点Q、N分别为两线段PE、PD上的动点，联结QD、QN，请直接写出QD+QN的最小值．