如图,在边长为1的小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,判断△ABC和△DEF是否相似,并说明理由;
如图1,在平面直角坐标系中,抛物线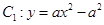 (
(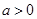 )经过点
)经过点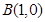 ,顶点为
,顶点为 .
.
(1)求抛物线 的解析式;
的解析式;
(2)如图2,先将抛物线 向上平移使其顶点在原点
向上平移使其顶点在原点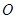 ,再将其顶点沿直线
,再将其顶点沿直线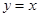 平移得到抛物线
平移得到抛物线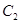 ,设抛物线
,设抛物线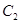 与直线
与直线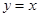 交于
交于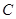 、
、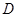 两点,求线段
两点,求线段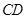 的长.
的长.
(3)在图1中将抛物线 绕点
绕点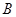 旋转
旋转 后得到抛物线
后得到抛物线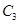 ,直线
,直线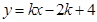 总经过一个定点
总经过一个定点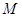 ,若过定点
,若过定点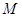 的直线
的直线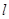 与抛物线
与抛物线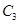 只有一个公共点,求直线
只有一个公共点,求直线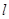 的解析式.
的解析式.
(本题10分)如图①,在Rt△ABC中,∠ACB-90°,AC=BC,CD⊥AB于点D,(1)把Rt△DBC绕点D顺时针旋转45°,点C的对应点为E,点B的对应点为F,请画出△EDF,连接AE、BE,并求出∠AEB的度数。
(2)如图 ,把
,把 绕点
绕点 顺时针旋转
顺时针旋转 度(
度( ),点
),点 的对应点为
的对应点为 ,点
,点 的对应点为
的对应点为 ,连接
,连接 ,求出
,求出 的度数,并写出线段
的度数,并写出线段 、
、 与
与 之间的数量关系,不证明。(2+3=5分)
之间的数量关系,不证明。(2+3=5分)
(3)如图 在(2)的条件下,连接
在(2)的条件下,连接 交
交 于点
于点 ,若
,若 ,
, ,则
,则 =_____________.(直接写出结果,不用证明)
=_____________.(直接写出结果,不用证明)

武汉某公司策划部进行调查后发现:如果单独投资A种产品,则所获利润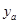 (万元)与投资金额
(万元)与投资金额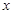 (万元)之间的关系图像如图1所示;如果单独投资B种产品,则所获利润
(万元)之间的关系图像如图1所示;如果单独投资B种产品,则所获利润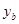 (万元)与投资金额
(万元)与投资金额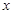 (万元)之间的关系图像如图2所示.
(万元)之间的关系图像如图2所示.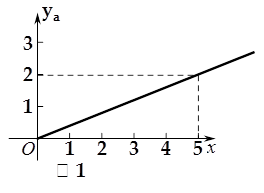
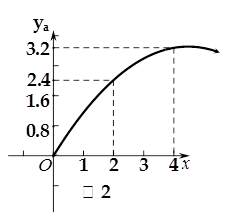
(1)请分别求出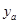 、
、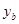 与
与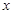 之间的函数表达式;
之间的函数表达式;
(2)若公司计划A、B两种产品共投资10万元,请你帮助该公司设计一个能获得最大利润的投资方案,并求出此方案所获得的最大利润.
如图,⊙O的直径AB为10,弦BC为6,D、E分别为 ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE.
ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE.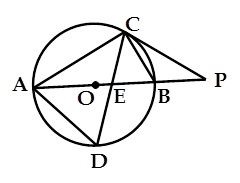
(1)求AC、AD的长;
(2)试判断直线PC与⊙O的位置关系,并说明理由;
(3)直接写出CD的长为____________.