四川雅安发生地震后,某校学生会向全校1900名学生发起了“心系雅安”捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图①和图②,请根据相关信息,解答下列是问题:

(Ⅰ)本次接受随机抽样调查的学生人数为 ,图①中m的值是 ;
(Ⅱ)求本次调查获取的样本数据的平均数、众数和中位数;
(Ⅲ)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.
为了了解某校初中男生的身体素质状况,在该校六年级至九年级共四个年级的男生中,分别抽取部分学生进行“引体向上”测试.所有被测试者的“引体向上”次数情况如表一所示;各年级的被测试人数占所有被测试人数的百分率如图5所示(其中六年级相关数据未标出).
| 次数 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 人数 |
1 |
1 |
2 |
2 |
3 |
4 |
2 |
2 |
2 |
0 |
1 |
表一
根据上述信息,回答下列问题(直接写出结果):
(1)六年级的被测试人数占所有被测试人数的百分率是
(2)在所有被测试者中,九年级的人数是 ;
(3)在所有被测试者中,“引体向上”次数不小于6的人数所占的百分率是 ;
(4)在所有被测试者的“引体向上”次数中,众数是
如图,一艘渔船位于海洋观测站P的北偏东60°方向,渔船在A处与海洋观测站P的距离为60海里,它沿正南方向航行一段时间后,到达位于海洋观测站P的南偏东45°方向上的B处。求此时渔船所在的B处与海洋观测站P的距离(结果保留根号)。
|

已知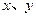 满足
满足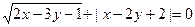 ,求
,求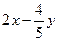 的平方根.
的平方根.
今年十月份,为方便民众出行,连江县成立了出租车公司,收费标准是:起步价5元,可乘坐3千米;3千米之后每千米加收1.8元.若某人乘坐了x千米,
(1)用代数式表示他应支付的费用;
(2)若他乘坐了13千米,应支付多少元?