计算: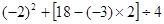
已知四边形ABCD中,AB∥CD,∠A=∠D=90°,AD=CD=4,AB=7.
现有M、N两点同时以相同的速度从A点出发,点M沿A—B—C-D方向前进,点N沿A—D—C-B方向前进,直到两点相遇时停止.设点M前进的路程为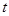 ,△AMN的面积为
,△AMN的面积为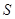 .
.
(1)试确定△AMN存在时,路程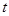 的取值范围.
的取值范围.
(2)请你求出面积S关于路程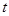 的函数.
的函数.
(3)当点M前进的路程为多少时,△AMN的面积最大?最大是多少?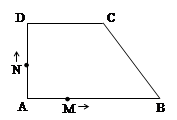


如图,AB为⊙O的直径,C是⊙O上一点,D在AB的延长线上,且∠DCB=∠A.
(1)CD与⊙O相切吗?如果相切,请你加以证明,如果不相切,请说明理由.
(2)若CD与⊙O相切,且∠D=30°,BD=8,求⊙O的半径.
A、B两位高尔夫球运动员10轮比赛成绩如下(单位:杆):
A运动员:73,73,74,75,75,76,76,77,79,79;
B运动员:75,75,75,75,76,76,76,77,77,77.
(1)计算两位运动员成绩的平均数;
(2)计算两位运动员成绩的极差;
(3)你认为谁是较优秀的运动员?谁是较稳定的运动员?简述理由.
经营一批进价为2元一件的小商品,在市场营销中发现此商品的日销售单价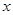 (元)与日销售量y(件)之间关系为y=
(元)与日销售量y(件)之间关系为y= ,而日销售利润P(元)与日销售单价
,而日销售利润P(元)与日销售单价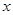 (元)之间的关系为P=
(元)之间的关系为P=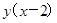 .当日销售单价为多少时,每日获得利润48元,且保证日销售量不低于10件?
.当日销售单价为多少时,每日获得利润48元,且保证日销售量不低于10件?