一农民带上若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数与他手中持有的钱数(含备用零钱)的关系,如图所示,结合图象回答下列问题.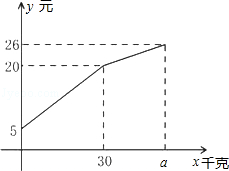
(1)农民自带的零钱是多少?
(2)试求降价前y与x之间的关系式?
(3)由表达式你能求出降价前每千克的土豆价格是多少?
(4)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,试问他一共带了多少千克土豆?
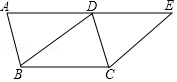
如图,四边形 是平行四边形,延长 至点 ,使 ,连接 .
(1)求证:四边形 是平行四边形;
(2)若 , ,求点 到点 的距离.
为了提高学生对毒品危害性的认识,我市相关部门每个月都要对学生进行“禁毒知识应知应会”测评.为了激发学生的积极性,某校对达到一定成绩的学生授予“禁毒小卫士”的荣誉称号.为了确定一个适当的奖励目标,该校随机选取了七年级20名学生在5月份测评的成绩,数据如下:
收集数据:90 91 89 96 90 98 90 97 91 98 99 97 91 88 90 97 95 90 95 88
(1)根据上述数据,将下列表格补充完整.
整理、描述数据:
|
成绩 分 |
88 |
89 |
90 |
91 |
95 |
96 |
97 |
98 |
99 |
|
学生人数 |
2 |
1 |
|
3 |
2 |
1 |
|
2 |
1 |
数据分析:样本数据的平均数、众数和中位数如下表
|
平均数 |
众数 |
中位数 |
|
93 |
|
91 |
得出结论:
(2)根据所给数据,如果该校想确定七年级前 的学生为“良好”等次,你认为“良好”等次的测评成绩至少定为 分.
数据应用:
(3)根据数据分析,该校决定在七年级授予测评成绩前 的学生“禁毒小卫士”荣誉称号,请估计评选该荣誉称号的最低分数,并说明理由.
如图,抛物线 与直线 分别相交于 , 两点,且此抛物线与 轴的一个交点为 ,连接 , .已知 , .
(1)求抛物线的解析式;
(2)在抛物线对称轴 上找一点 ,使 的值最大,并求出这个最大值;
(3)点 为 轴右侧抛物线上一动点,连接 ,过点 作 交 轴于点 ,问:是否存在点 使得以 , , 为顶点的三角形与 相似?若存在,请求出所有符合条件的点 的坐标;若不存在,请说明理由.

如图,在 中, ,以 为直径的 与边 , 分别交于 , 两点,过点 作 于点 .
(1)判断 与 的位置关系,并说明理由;
(2)求证: 为 的中点;
(3)若 , ,求 的长.

(1)如图①,在四边形 中, ,点 是 的中点,若 是 的平分线,试判断 , , 之间的等量关系.
解决此问题可以用如下方法:延长 交 的延长线于点 ,易证 得到 ,从而把 , , 转化在一个三角形中即可判断.
, , 之间的等量关系 ;
(2)问题探究:如图②,在四边形 中, , 与 的延长线交于点 ,点 是 的中点,若 是 的平分线,试探究 , , 之间的等量关系,并证明你的结论.
