已知:如图,OA、OB为⊙O的半径, C、D分别为OA、OB的中点,求证:AD=BC.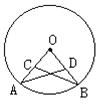
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后, 的顶点均在格点上,点
的顶点均在格点上,点 的坐标为
的坐标为 .
.
①把 向上平移5个单位后得到对应的
向上平移5个单位后得到对应的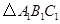 ,画出
,画出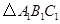 ,并写出
,并写出 的坐标;
的坐标;
②以原点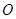 为对称中心,画出
为对称中心,画出 与关于原点
与关于原点 对称的
对称的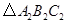 ,并写出点
,并写出点 的坐标.
的坐标.
③以原点O为旋转中心,画出把 顺时针旋转90°的图形△A3B3C3,并写出C3的坐标.
顺时针旋转90°的图形△A3B3C3,并写出C3的坐标.
有一个转盘游戏,被平均分成10份(如图4),分别标有1,2,……,10这10个数字,转盘上有固定的指针,转动转盘,当转盘停止转动时,指针指向的数字即为转出的数字.两人进行游戏,一人转动转盘,另一人猜数,如果猜的数与转出的数情况相符,则猜数的人获胜,否则转盘的人获胜.猜数的方法为下列三种中的一种: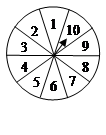
(1)猜奇数或偶数;
(2)猜是3的倍数或不是3的倍数;
(3)猜大于4的数或不大于4的数.
(4)如果你是猜数的游戏者,为了尽可能取胜,你选哪种猜法?怎样猜?
一个圆锥的底面半径为10cm,母线长20cm,求:
(1)圆锥的全面积(结果保留π);
(2)圆锥的高;
已知关于x的方程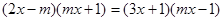 有一个根是0,求另一个根和
有一个根是0,求另一个根和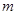 的值.
的值.