如图，直线AB的解析式为y=2x+4，交x轴于点A，交y轴于点B，以A为顶点的抛物线交直线AB于点D，交y轴负半轴于点C（0，-4）．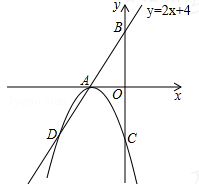
（1）求抛物线的解析式；
（2）将抛物线顶点沿着直线AB平移，此时顶点记为E，与y轴的交点记为F，
①求当△BEF与△BAO相似时，E点坐标；
②记平移后抛物线与AB另一个交点为G，则S△EFG与S△ACD是否存在8倍的关系？若有请直接写出F点的坐标．
已知方程组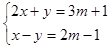
，试列出使x＞y成立的关于m的不等式．
某市自来水公司按如下标准收取水费：若每户每月用水不超过10m3，则每立方米收费1.5元；若每户每月用水超过10m3，则超过的部分每立方米收费2元．小亮家某月的水费不少于25元，那么他家这个月的用水量（xm3）至少是多少？请列出关于x的不等式．
某学校为学生安排宿舍，现有住房若干间，若每间5人，则还有14人安排不下，若每间7人，则有一间不足7人．问学校至少有几间房可以安排学生住宿？可以安排住宿的学生有多少人？
（1）列式：x与20的差不小于0；
（2）若（1）中的x（单位：cm）是一个正方形的边长，现将正方形的边长增加2cm，则正方形的面积至少增加多少？
已知：一个数a的平方根是2b-3和3b+8，求a、b的值．