如图所示,正四棱锥 中,
中, 为底面正方形的中心,侧棱
为底面正方形的中心,侧棱 与底面
与底面 所成的角的正切值为
所成的角的正切值为 .
.
(1)求侧面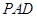 与底面
与底面 所成的二面角的大小;
所成的二面角的大小;
(2)若 是
是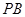 的中点,求异面直线
的中点,求异面直线 与
与 所成角的正切值;
所成角的正切值;
(3)问在棱 上是否存在一点
上是否存在一点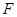 ,使
,使 ⊥侧面
⊥侧面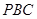 ,若存在,试确定点
,若存在,试确定点 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
某港口水的深度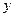 (米)是时间
(米)是时间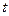 (
(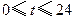 ,单位:时)的函数,记作
,单位:时)的函数,记作 ,下面是某日水深的数据:
,下面是某日水深的数据:
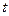 (时) (时) |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
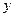 (米) (米) |
10.0 |
13.0 |
9.9 |
7.0 |
10.0 |
13.0 |
10.1 |
7.0 |
10.0 |
经长期观察, 的曲线可以近似地看成函数
的曲线可以近似地看成函数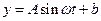 .
.
⑴试根据以上数据,求出函数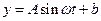 的最小正周期、振幅和表达式;
的最小正周期、振幅和表达式;
⑵一般情况下,船舶航行时,船底离海底的距离为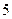 米或
米或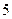 米以上时认为安全的(船舶停靠时,船底只须不碰海底即可).某船吃水深度(船底离水面的距离)为
米以上时认为安全的(船舶停靠时,船底只须不碰海底即可).某船吃水深度(船底离水面的距离)为 米.如果该船希望在同一天内安全进出港,请问,它至多能在港内停留多长
米.如果该船希望在同一天内安全进出港,请问,它至多能在港内停留多长
时间(忽略进出港所需的时间)?
已知 ,
,
(1)求 的最小正周期;
的最小正周期;
(2)若 ,求
,求 的最大值、最小值.
的最大值、最小值.
求函数 的最大值和最小值.
的最大值和最小值.
设 在
在 上是偶函数,在区间
上是偶函数,在区间 上递增,且有
上递增,且有 ,求
,求 的取值范围.
的取值范围.
求函数 的值域.
的值域.