利用水流和太阳能发电,可以为人类提供清洁能源。水的密度ρ=1×103kg/m3,太阳光垂直照射到地面上时的辐射功率P0 =1×103W/m2,地球半径为R=6.4×106m,地球表面的重力加速度取g=10m/s2。
⑴写出太阳光照射到地球表面的总功率P的字母表达式;
⑵发射一颗卫星到地球同步轨道上(轨道半径约为地球半径的6.6≈ 倍)利用太阳能发电,然后通过微波持续不断地将电力输送到地面,这样就建成了太阳能发电站。求卫星在地球同步轨道上向心加速度的大小(答案保留两位有效数字);
倍)利用太阳能发电,然后通过微波持续不断地将电力输送到地面,这样就建成了太阳能发电站。求卫星在地球同步轨道上向心加速度的大小(答案保留两位有效数字);
⑶三峡水电站水库面积约为S=1×109m2,平均流量Q=1.5×104m3/s,水库水面与发电机所在位置的平均高度差为h=100m,发电站将水的势能转化为电能的总效率η1=60%。在地球同步轨道上,太阳光垂直照射时的辐射功率为1.4P0。太阳能电池板将太阳能转化为电能的效率为η2=20%,将电能输送到地面的过程要损失50%。若要使⑵中的太阳能发电站在被太阳照射时地面接收到的电功率相当于三峡电站发电的平均功率,卫星上太阳能电池板的面积应为多大?(保留一位有效数字)
放在水平面上的物体,与水平面间的动摩擦因数为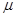 ,物体在水平恒力F1的作用下,在水平面上作匀速直线运动,今若再对物体施加一大小与F1相等的恒力F2后,要使物体仍然能沿原速度方向在水平面上作匀速直线运动,那么力F2的方向应满足什么条件?
,物体在水平恒力F1的作用下,在水平面上作匀速直线运动,今若再对物体施加一大小与F1相等的恒力F2后,要使物体仍然能沿原速度方向在水平面上作匀速直线运动,那么力F2的方向应满足什么条件?
一辆值勤的警车停在公路边,当警员发现从他旁边以10m/s的速度匀速行驶的货车严重超载时,决定前去追赶,经过5.5s后警车发动起来,并以2.5m/s2的加速度做匀加速运动,但警车的行驶速度必须控制在90km/h以内.问:
(1)警车在追赶货车的过程中,两车间的最大距离是多少?
(2)警车发动后要多长时间才能追上货车?
质量为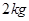 的物体在水平推力
的物体在水平推力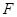 的作用下沿水平面作直线运动,一段时间后撤去
的作用下沿水平面作直线运动,一段时间后撤去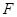 ,其运动的
,其运动的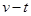 图像如图所示。
图像如图所示。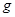 取
取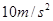 ,求:
,求:
(1)物体与水平面间的运动摩擦因数
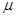 ;
;
(2)水平推力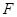 的大小;
的大小;
(3)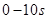 内物体运动位移的大小。
内物体运动位移的大小。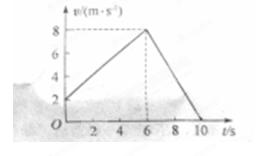
跳伞运动员做低空跳伞表演,他离开飞机后先做自由落体运动,当距离地面 125 m时打开降落伞,伞张开后运动员就以14.3 m/s2的加速度做匀减速运动,到达地面时速度为5 m/s,问:
(1)运动员离开飞机时距地面的高度为多少?
(2)离开飞机后,经过多少时间才能到达地面?(g="10" m/s2)
一传送带与水平面夹角为370,顶到底长为12.8m,以4m/s匀速向下运动。现将一物块轻轻从顶端放在带上,物块与带间动摩擦因数为0.5,求从顶运动到底端的时间。
(取g=10m/s2、sin370=0.6、cos370=0.8)