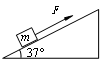
如图所示,在倾角θ=37°的足够长的固定斜面上,有一质量m=1.0kg的物体,其与斜面间动摩擦因数μ=0.25。物体受到平行于斜面向上F=9.0N的拉力作用,从静止开始运动,经时间t=8.0s绳子突然断裂。若已知sin37º=0.60,cos37º=0.80,g取10m/s2。试分析求解:
(1)绳断时物体的速度大小;
(2)从绳子断裂开始到物体再返回到斜面底端的运动时间。
如图所示,MN与PQ为在同一水平面内的平行光滑金属导轨,间距l=0.5m,电阻不计,在导轨左端接阻值为R=0.6Ω的电阻.整个金属导轨置于竖直向下的匀强磁场中,磁感应强度大小为B=2T.将质量m=1kg、电阻r=0.4Ω的金属杆ab垂直跨接在导轨上.金属杆ab在水平拉力F的作用下由静止开始向右做匀加速运动.开始时,水平拉力为F0=2N.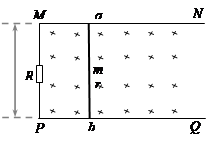
(1)求金属杆ab的加速度大小;
(2)求2s末回路中的电流大小;
(3)已知开始2s内电阻R上产生的焦耳热为6.4J,求该2s内水平拉力F所做的功.
一质量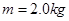 的小物块以一定的初速度冲上一足够长的斜面,斜面的倾角
的小物块以一定的初速度冲上一足够长的斜面,斜面的倾角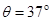 .某同学利用传感器测出了小物块从一开始冲上斜面上滑过程中多个时刻的瞬时速度,并用计算机作出了小物块上滑过程的速度—时间图线,如图所示.(已知重力加速度
.某同学利用传感器测出了小物块从一开始冲上斜面上滑过程中多个时刻的瞬时速度,并用计算机作出了小物块上滑过程的速度—时间图线,如图所示.(已知重力加速度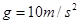 ,
,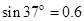 ,
,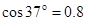 )求:
)求: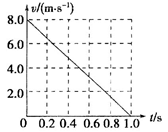
(1)小物块冲上斜面过程中加速度的大小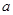 ;
;
(2)小物块与斜面间的动摩擦因数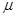 ;
;
(3)小物块沿斜面上滑的过程中克服摩擦阻力做的功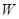 .
.
有一个竖直固定在地面的透气圆筒,筒中有一劲度系数为 的轻弹簧,其下端固定,上端连接一质量为
的轻弹簧,其下端固定,上端连接一质量为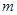 的薄滑块,圆筒内壁涂有一层新型智能材料─—ER流体,它对滑块的阻力可调。起初,滑块静止,ER流体对其阻力为0,弹簧的长度为L.现有一质量也为
的薄滑块,圆筒内壁涂有一层新型智能材料─—ER流体,它对滑块的阻力可调。起初,滑块静止,ER流体对其阻力为0,弹簧的长度为L.现有一质量也为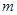 的物体从距地面2L处自由落下,与滑块碰撞后粘在一起向下运动。为保证滑块做匀减速运动,且下移距离为
的物体从距地面2L处自由落下,与滑块碰撞后粘在一起向下运动。为保证滑块做匀减速运动,且下移距离为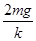 时速度减为0,ER流体对滑块的阻力须随滑块下移而变。试求(忽略空气阻力):
时速度减为0,ER流体对滑块的阻力须随滑块下移而变。试求(忽略空气阻力):
(1)下落物体与滑块碰撞前的瞬间物体的速度;
(2)下落物体与滑块碰撞过程中系统损失的机械能;
(3)滑块下移距离d时ER流体对滑块阻力的大小。
如图所示,长度为l的轻绳上端固定在O点,下端系一质量为m的小球(小球的大小可以忽略)。
(1)在水平拉力F的作用下,轻绳与竖直方向的夹角为α,小球保持静止。画出此时小球的受力图,并求力F的大小;
(2)由图示位置无初速释放小球,求当小球通过最低点时的速度大小及轻绳对小球的拉力。不计空气阻力。
节能混合动力车是一种可以利用汽油及所储存电能作为动力来源的汽车。有一质量m=1000kg的混合动力轿车,在平直公路上以 匀速行驶,发动机的输出功率为
匀速行驶,发动机的输出功率为 。当驾驶员看到前方有80km/h的限速标志时,保持发动机功率不变,立即启动利用电磁阻尼带动的发电机工作给电池充电,使轿车做减速运动,运动L=72m后,速度变为
。当驾驶员看到前方有80km/h的限速标志时,保持发动机功率不变,立即启动利用电磁阻尼带动的发电机工作给电池充电,使轿车做减速运动,运动L=72m后,速度变为 。此过程中发动机功率的
。此过程中发动机功率的 用于轿车的牵引,
用于轿车的牵引, 用于供给发电机工作,发动机输送给发电机的能量最后有50%转化为电池的电能。假设轿车在上述运动过程中所受阻力保持不变。求
用于供给发电机工作,发动机输送给发电机的能量最后有50%转化为电池的电能。假设轿车在上述运动过程中所受阻力保持不变。求
(1)轿车以 在平直公路上匀速行驶时,所受阻力
在平直公路上匀速行驶时,所受阻力 的大小;
的大小;
(2)轿车从 减速到
减速到 过程中,获得的电能
过程中,获得的电能 ;
;
(3)轿车仅用其在上述减速过程中获得的电能 维持
维持 匀速运动的距离
匀速运动的距离 。
。