（1）先化简，再求值：
，其中x=2015．
（2）如图，某广场设计的一建筑物造型的纵截面是抛物线的一部分，抛物线的顶点O落在水平面上，对称轴是水平线OC，点A、B在抛物线造型上，且点A到水平面的距离AC=4米，点B到水平面的距离为2米，OC=8米．
①请建立适当的直角坐标系，求抛物线的函数解析式；（需要画出你建立的直角坐标系）
②为了安全美观，现需要在水平线OC上找一点P，用质地、规格已确定的圆形钢管制作两根支柱PA、PB对抛物线造型进行支撑加固，那么怎样才能找到两根支柱用料最省时的点P？请写出找法．（无需证明）（支柱与地面、造型对接方式的用料多少问题暂不考虑）
如图所示，正方形
是以金属丝围成的，其边长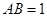
，把此正方形的金属丝重新围成扇形的
，使
，
不变，问正方形面积与扇形面积谁大？大多少？由计算得出结果．
如图正方形ABCD边长为1，G为CD边上的一个动点（点G与C、D不重合），以CG为一边向正方形ABCD外作正方形GCEF，连接DE交BG的延长线于点H。
（1）求证：BH⊥DE；
（2）当BH垂直平分DE时，求CG的长度？请说明理由。
某水果批发商场经销一种高档水果，如果每千克盈利10元，每天可售出500千克，经市场调查发现，在进货价不变的情况下，若每千克涨价为1元，日销售量将减少20千克，现该商场要保证每天盈利6000元，同时又要使顾客得到实惠，那么每千克应涨价多少元？
（6分)王阿姨绣了一幅长80㎝，宽50㎝的十字绣风景画，在裱画时，画的四周镶上宽度相等的金边，为了使整幅画的面积达到5400㎝2，问金边的宽度是多少？
四边形ABCD中，AD=BC，AE⊥BD，CF⊥BD，垂足为E、F，BE =DF，
求证：四边形ABCD是平行四边形。