如图，已知抛物线C1与坐标轴的交点依次是A（-4，0），B（-2，0），E（0，8）．
（1）求抛物线C1关于原点对称的抛物线C2的解析式；
（2）设抛物线C1的顶点为M，抛物线C2与x轴分别交于C，D两点（点C在点D的左侧），顶点为N，四边形MDNA的面积为S．若点A，点D同时以每秒1个单位的速度沿水平方向分别向右、向左运动；与此同时，点M，点N同时以每秒2个单位的速度沿坚直方向分别向下、向上运动，直到点A与点D重合为止．求出四边形MDNA的面积S与运动时间t之间的关系式，并写出自变量t的取值范围；
（3）当t为何值时，四边形MDNA的面积S有最大值，并求出此最大值；
（4）在运动过程中，四边形MDNA能否形成矩形？若能，求出此时t的值；若不能，请说明理由．
．已知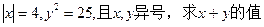
两船从同一港口同时出发反向而行，甲船顺水，乙船逆水，两船在静水中的速度都是50千米 /时，水流速度是
千米/时，3小时后两船相距多远？
有
筐白菜，以每筐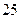
千克为标准，超过的千克数记作正数，不足的千克数记作负数，称后的纪录如下：
回答下列问题：
（1）这筐白菜中最接近标准重量的这筐白菜重千克；
（2）这筐白菜一共重多少千克？
观察下面三行数：
-2， 4， -8， 16， -32， 64，……①
0, 6, -6, 18, -30, 66, ……②
-1, 2, -4, 8, -16, 32, ……③
(1)第①行数的第21个数是（可用幂的形式表示）
第②行数的第21个数是
第③行数的第21个数是
(2)若第①行数的某个数为x，它与第②行数、第③行数中与它相对应的数的和
为-318，求x
某商店出售茶杯、茶壶，茶杯每只定价4元，茶壶每只定价20元，该商店的优惠办法
是买一只茶壶赠一只茶杯，某顾客欲购买茶壶5只，茶杯
只（茶杯数超过5只）。
（1）用含的式子表示这位顾客应付款的钱数；
（2）当
时，应付款多少元？