罗非鱼又名非洲鲫鱼,是一种中小型鱼,每年的10月份是罗非鱼的捕捞期,某渔民有两个罗非鱼养殖鱼塘,在捕捞前期,为了估计鱼塘中罗非鱼的质量,该渔民从第一个鱼塘中随机捕捞若干条罗非鱼称得它们的质量(单位;kg),并将所得的数据绘制成了如图1图2所示的统计图(不完整)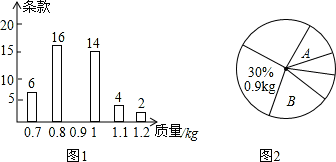
(1)求该渔民所捞的罗非鱼的质量平均数、中位数和众数.
(2)当此渔民将罗非鱼的质量数据绘制成如图2所示的扇形统计图时,因某些原因没有标完数据,他只记得A扇形的圆心为36°,B扇形的中心角为84°,求A,B两个扇形分别表示的是哪种质量的罗非鱼;
(3)在同一时期,该渔民在第二个鱼塘捕捞了和第一个鱼塘相同条数的罗非鱼,并且求出罗非鱼质量的平均数也和第一个鱼塘的相同,但该鱼塘所捕捞的罗非鱼的质量的方差比第一个鱼塘的方差小,试判断哪个鱼塘的罗非鱼的质量的波动性较小.
(本题满分12分) 如图所示, 在平面直角坐标系xoy中, 矩形OABC的边长OA、OC分别为12cm、6cm, 点A、C分别在y轴的负半轴和x轴的正半轴上, 抛物线y=ax2+bx+c经过点A、B, 且18a + c = 0.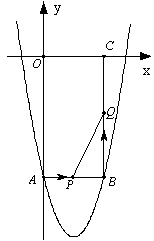
(1)求抛物线的解析式.
(2)如果点P由点A开始沿AB边以1cm/s的速度向终点B移动, 同时点Q由点B开始沿BC边以2cm/s的速度向终点C移动.
①移动开始后第t秒时, 设△PBQ的面积为S, 试写出S与t之间的函数关系式, 并写出t的取值范围.
②当S取得最大值时, 在抛物线上是否存在点R, 使得以P、B、Q、R为顶点的四边形是平行四边形? 如果存在, 求出R点的坐标, 如果不存在, 请说明理由.
(本题满分12分) 如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
(1)求证:PC是⊙O的切线;
(2)求∠P的度数;
(3)点M是弧AB的中点,CM交AB于点N,AB=4,求线段BM、CM及弧BC所围成的图形面积。
(本题满分10分) 今年“五一”期间,小明准备攀登海拔高度为2000米的山峰。导游介绍山区气温会随着海拔高度的增加而下降,提醒大家上山要多带一件衣服,小明从网上查到该山区海拔和即时气温的部分数据表,数据如下:
| 海拔高度x(米) |
400 |
500 |
600 |
700 |
800 |
…… |
| 气温y(°C) |
29.2 |
28.6 |
28.0 |
27.4 |
26.8 |
…… |
(1)以海拔高度为x轴,根据上表提供的数据在下列直角坐标系中描点并连线;

(2)观察(1)中所画出的图象,猜想与之间函数关系,求出所猜想的函数关系表达式,并根据表中提供的数据验证你的猜想;
(3)如果气温低于200C就需要穿外套,请问小明需不需要携带外套上山?
(本题满分10分)
学习投影后,小刚、小雯利用灯光下自己的影子长度来测量一路灯的高度。如图,在同一时间,身高为1.6m的小刚(AB)的影子BC长是3m,而小雯(EH)刚好在路灯灯泡的正下方 点,并测得HB=6m.
点,并测得HB=6m.
(1)请
 在图中画出形成影子的光线,并确定路灯灯泡所在的位置G;
在图中画出形成影子的光线,并确定路灯灯泡所在的位置G;(2)求路灯灯泡的垂直高度GH;
(3)如果小刚沿线段BH向小雯(点H)走去,当小明走到BH中点B1处时,求其影子B1C1的长。
(本题满分10分)如图,△ABC的三个顶点都在格点上.A(-1,3), B(-1,-1), C(-3,-3)
(1)画出△ABC绕点A逆时针旋转90°所得图形△AB'C'
(2)直接写出△AB'C'外接圆的圆心D坐标
 .
.(3)求∠A C'B'的正切值.