如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:
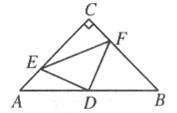
①△DFE是等腰直角三角形;
②四边形CEDF不可能为正方形;
③四边形CEDF的面积随点E位置的改变而发生变化;
④点C到线段EF的最大距离为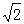 。
。
其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
如图,在△ABC中,点D、E、F分别在BC、AB、CA上,且DE∥CA,DF∥BA,则下列三种说法: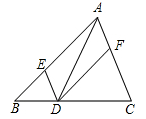
(1)如果∠BAC=90°,那么四边形AEDF是矩形
(2)如果AD平分∠BAC,那么四边形AEDF是菱形
(3)如果AD⊥BC且AB=AC,那么四边形AEDF是正方形 .其中正确的有 ()
A.3个 B.2个 C.1个 D.0个
如图,过□ABCD的对角线BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中的□AEMG的面积S1与□HCFM的面积S2的大小关系是 ()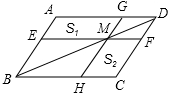
| A.S1> S2 | B.S1= S2 | C.S1<S2 | D.不能确定 |
菱形具有而一般平行四边形不具有的性质是 ()
| A.对边相等 | B.对角相等 |
| C.对角线互相垂直 | D.对角线互相平分 |
已知点A与点(−4 ,−5)关于y轴对称,则A点坐标是 ()
| A.(4 ,−5) | B.(−4 ,5) | C.(−5 ,−4) | D.(4 ,5) |
已知x2−5xy+6y2=0,则x∶y等于 ()
A. 或 或 |
B.2或3 | C. 或1 或1 |
D.6或1 |