为了解甲、乙两种车的刹车距离,经试验发现,甲车的刹车距离s甲是车速v的 ,乙车的刹车距离s乙等于反应距离与制动距离之和,二反应距离与车速v成正比,制动距离与车速v2成正比,具体关系如下表:
,乙车的刹车距离s乙等于反应距离与制动距离之和,二反应距离与车速v成正比,制动距离与车速v2成正比,具体关系如下表:
| 车速v(km/h) |
40 |
50 |
| 刹车距离s乙(m) |
12 |
17.5 |
(1)分别求出s甲、s乙与车速v的函数关系式;
(2)若乙车在限速120km/h的高速公路上行驶,乙车的最长刹车距离是多少m?
(3)刹车速度是处理交通事故的一个重要因素,请看下面一个交通事故案例:甲、乙两车在限速为80km/g的道路上相向而行,等望见对方,同时刹车时已晚,两车还是相撞了,事后经现场勘查,测得甲车的刹车距离超过16m,但小于18m,乙车的刹车距离是24m,请你比较两车的速度,并判断哪辆车超速?
如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC.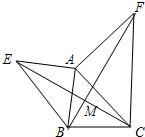
求证:(1)EC=BF;(2)EC⊥BF.
如图所示,△ABC≌△ADE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,求∠DFB和∠DGB的度数.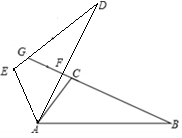
如图所示,四边形ABCD的对角线AC,BD相交于点O,△ABC≌△BAD.
求证:(1)OA=OB;(2)AB∥CD.
某车间有甲、乙两条生产线.在甲生产线已生产了200吨成品后,乙生产线开始投入生产,甲、乙两条生产线每天分别生产20吨和30吨成品.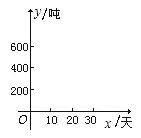
(1)分别求出甲、乙两条生产线各自总产量 (吨)与从乙开始投产以来所用时间
(吨)与从乙开始投产以来所用时间 (天)之间的函数关系式.
(天)之间的函数关系式.
(2)作出上述两个函数在如图所示的直角坐标系中的图象,观察图象,分别指出第10天和第30天结束时,哪条生产线的总产量高?
为保护学生视力,课桌椅的高度都是按一定的关系配套设计的,研究表明:假设课桌的高度为 cm,椅子的高度为
cm,椅子的高度为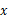 cm,则
cm,则 应是
应是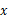 的一次函数,下表列出两套符合条件的课桌椅的高度:
的一次函数,下表列出两套符合条件的课桌椅的高度:
| 第一套 |
第二套 |
|
椅子高度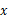 (cm) (cm) |
40 |
37 |
课桌高度 (cm) (cm) |
75 |
70 |
(1)请确定 与
与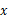 的函数关系式.
的函数关系式.
(2)现有一把高39 cm的椅子和一张高78.2 cm的课桌,它们是否配套?为什么?