问题发现:
如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.
(1)求证:△ACD≌△BCE;
(2)求证:CD∥BE.
拓展探究:
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,连接BE,求∠AEB的度数.
二次函数y=ax2+bx+c(a≠0)的图象与x轴的交点为A(﹣3,0)、B(1,0)两点,与y轴交于点C(0,﹣3m)(其中m>0),顶点为D.
(1)求该二次函数的解析式(系数用含m的代数式表示);
(2)如图①,当m=2时,点P为第三象限内的抛物线上的一个动点,设△APC的面积为S,试求出S与点P的横坐标x之间的函数关系式及S的最大值;
(3)如图②,当m取何值时,以A、D、C为顶点的三角形与△BOC相似?
如图,已知直线AB分别交x轴、y轴于点A(﹣4,0)、B(0,3),点P从点A出发,以每秒1个单位的速度沿直线AB向点B移动,同时,将直线 以每秒0.6个单位的速度向上平移,分别交AO、BO于点C、D,设运动时间为t秒(0<t<5).
以每秒0.6个单位的速度向上平移,分别交AO、BO于点C、D,设运动时间为t秒(0<t<5).
(1)证明:在运动过程中,四边形ACDP总是平行四边形;
(2)当t取何值时,四边形ACDP为菱形?且指出此时以点D为圆心,以DO长为半径的圆与直线AB的位置关系,并说明理由.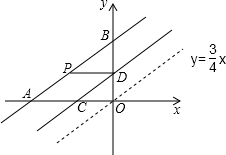
将一副三角尺(在Rt△ABC中,∠ACB=90°,∠B=60°,在Rt△DEF中,∠EDF=90°,∠E=45°)如图①摆放,点D为AB的中点,DE交AC于点P,DF经过点C.
(1)求∠ADE的度数;
(2)如图②,将△DEF绕点D顺时针方向旋转角α(0°<α<60°),此时的等腰直角三角尺记为△DE′F′,DE′交AC于点M,DF′交BC于点N,试判断 的值是否随着α的变化而变化?如果不变,请求出
的值是否随着α的变化而变化?如果不变,请求出 的值;反之,请说明理由.
的值;反之,请说明理由.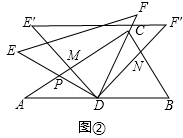
某班组织班团活动,班委会准备用15元钱全部用来购买笔记本和中性笔两种奖品,已知笔记本2元/本,中性笔1元/支,且每种奖品至少买1件.
(1)若设购买笔记本x本,中性笔y支,写出y与x之间的关系式;
(2)有多少种购买方案?请列举所有可能的结果;
(3)从上述方案中任选一种方案购买,求买到的中性笔与笔记本数量相等的概率.
学校去年年底的绿化面积为5000平方米,预计到明年年底增加到7200平方米,求这两年的年平均增长率.