某校为了开设武术、舞蹈、剪纸等三项活动课程以提升学生的体艺素养，随机抽取了部分学生对这三项活动的兴趣情况进行了调查（每人从中只能选一项），并将调查结果绘制成如图两幅统计图，请你结合图中信息解答问题．
（1）将条形统计图补充完整；
（2）本次抽样调查的样本容量是 ；
（3）已知该校有1200名学生，请你根据样本估计全校学生中喜欢剪纸的人数．
解方程：x2＋2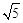
x―4=0．
解方程：（1）x2＋x―12=0；
如图，BD平分∠ABC，且AB=4，BC=6，则当BD=时，△ABD∽△DBC．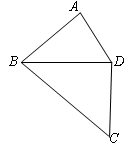
已知二次函数y1=ax2+bx+c（a≠0）与一次函数y2=mx+n（m≠0）的图象相交于点A（―2，4），B（8，2），如图所示，则能使y1＜y2成立的x的取值范围是．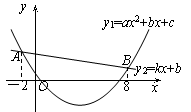
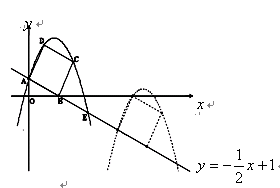
如图，已 知直线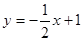 
交坐标轴于
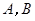两点，以线段
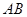为边向上作正方形
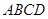，过点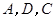
的抛物线与直线另一个交点为
．
（1）请直接写出点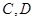
的坐标；
（2）求抛物线的解析式；
（3）若正方形以每秒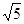
个单位长度的速度沿射线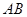下滑，直至顶点
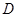落在x轴上时停止．设正方形落在
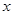轴下方部分的面积为
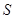，求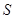关于滑行时间
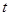的函数关系式，并写出相应自变量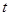的取值范围；
（4）在（3）的条件下，抛物线与正方形一起平移，同时停止，求抛物线上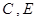
两点间的抛物线弧所扫过的面积．