(本小题共14分)张先生家住H小区,他在C科技园区工作,从家开车到公司上班有L1,L2两条路线(如图),L1路线上有A1,A2,A3三个路口,各路口遇到红灯的概率均为 ;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为
;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为 ,
, .
.
(Ⅰ)若走L1路线,求最多遇到1次红灯的概率;
(Ⅱ)若走L2路线,求遇到红灯次数 的数学期望;
的数学期望;
(Ⅲ)按照“平均遇到红灯次数最少”的要求,请你帮助张先生从上述两条路线中选择一条最好的上班路线,并说明理由.
一个人在建筑物的正西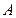 点,测得建筑物顶的仰角是
点,测得建筑物顶的仰角是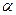 ,这个人再从
,这个人再从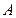 点向南走到
点向南走到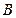 点,再测得建筑物顶的仰角是
点,再测得建筑物顶的仰角是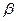 ,设
,设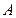 ,
,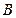 间的距离是
间的距离是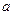 .
.
证明:建筑物的高是 .
.
测山上石油钻井的井架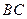 的高,从山脚
的高,从山脚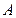 测得
测得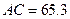 m,塔顶
m,塔顶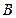 的仰角
的仰角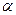 是
是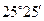 .已知山坡的倾斜角是
.已知山坡的倾斜角是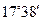 ,求井架的高
,求井架的高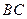 .
.
如图,货轮在海上以35n mile / h的速度沿着方位角(从指北方向顺时针转到目标方向线的水平角)为 的方向航行.为了确定船位,在B点观察灯塔A的方位角是
的方向航行.为了确定船位,在B点观察灯塔A的方位角是 ,航行半小时后到达C点,观察灯塔A的方位角是
,航行半小时后到达C点,观察灯塔A的方位角是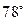 .求货轮到达C点时与灯塔A的距离(精确到1 n mile).
.求货轮到达C点时与灯塔A的距离(精确到1 n mile).
 |
如图,在山脚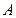 测得出山顶
测得出山顶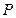 的仰角为
的仰角为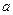 ,沿倾斜角为
,沿倾斜角为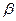 的斜坡向上走
的斜坡向上走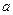 米到
米到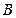 ,在
,在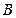 处测得山顶
处测得山顶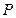 的仰角为
的仰角为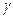 ,求证:山高
,求证:山高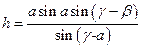 .
.
 |
为测量某塔的高度,在A、B两点进行测量的数据如图所示,求塔的高度.