一个人在建筑物的正西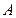
点，测得建筑物顶的仰角是
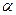，这个人再从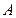点向南走到
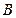点，再测得建筑物顶的仰角是
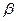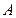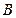，设，间的距离是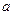
．
证明：建筑物的高是
．
如图，在四棱锥
中，
底面
，
， 
，
，
，点
为棱
的中点.
（Ⅰ）证明：
；
（Ⅱ）若
为棱上一点，满足
，求二面角
的余弦值.
已知
为定义在
上的奇函数，当
时，函数解析式为
.
（Ⅰ）求
的值，并求出在
上的解析式；
（Ⅱ）求在上的最值．
某中学社团部志愿者协会共有6名男同学，4名女同学. 在这10名同学中，3名同学来自动漫社，其余7名同学来自摄影社、话剧社等其他互不相同的七个社团. 现从这10名同学中随机选取3名同学，到社区参加志愿活动（每位同学被选到的可能性相同）.
（Ⅰ）求选出的3名同学是来自互不相同社团的概率；
（Ⅱ）设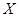
为选出的3名同学中女同学的人数，求随机变量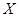的分布列和数学期望.
已知函数
，
.
（Ⅰ）求
的最小正周期；
（Ⅱ）求在闭区间
上的最大值和最小值.
已知函数
，其中
为实数，常数
.
(1) 若
是函数
的一个极值点，求的值；
(2) 当取正实数时，求函数的单调区间；
(3) 当
时，直接写出函数的所有减区间.