(本小题满分14分)已知半径为 的圆的圆心在
的圆的圆心在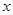 轴上,圆心的横坐标是整数,且与直线
轴上,圆心的横坐标是整数,且与直线 相切.
相切.
(Ⅰ)求圆的方程;
(Ⅱ)设直线
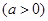 与圆相交于
与圆相交于 两点,求实数
两点,求实数 的取值范围;
的取值范围;
(Ⅲ) 在(Ⅱ)的条件下,是否存在实数 ,使得弦
,使得弦 的垂直平分线
的垂直平分线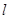 过点
过点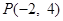 ,若存在,求出实数
,若存在,求出实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本小题满分12分)
已知定点 ,动点
,动点 满足
满足 。
。
(1)求动点 的轨迹方程,并说明方程表示的曲线;
的轨迹方程,并说明方程表示的曲线;
(2)当 时,求
时,求 的最大值和最小值。
的最大值和最小值。
(本小题满分12分)
已知函数
(1)求函数 的最大值,以及取到最大值时所对应的
的最大值,以及取到最大值时所对应的 的集合;
的集合;
(2) 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围。
的取值范围。
(本小题满分12分)口袋中装有质地大小完全的5个球,编号分别为1,2,3,4,5,甲、乙两人玩一种游戏:甲先摸一个球,记下编号,放回后乙再摸一个球,记下编号。如果两个编号的和为偶数就算甲胜,否则算乙胜。
(1)求甲胜且编号的和为6的事件发生的概率;
(2)这种游戏规则公平吗?说明理由。
(本小题满分12分)
已知向量 ,函数
,函数
(1)求 的单调递增区间;
的单调递增区间;
(2)当 时, 若
时, 若 求
求 的值。
的值。
(本小题满分12分)
已知向量 与
与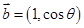 互相垂直,其中
互相垂直,其中 。
。
(1)求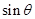 和
和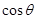 的值;
的值;
(2)若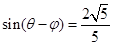 ,
,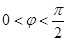 ,求
,求 的值。
的值。