(本小题满分12分)某单位对三个车间的人数统计情况如下表:用分层抽样的方法从三个车间抽取30人,其中三车间有12人.
| |
一车间 |
二车间 |
三车间 |
| 男职工 |
200 |
100 |
250 |
| 女职工 |
600 |
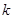 |
550 |
(Ⅰ)求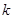 的值;
的值;
(Ⅱ)为了考察职工加班情况,从编号000~199中的一车间男职工中,用系统抽样法先后抽取5人的全年加班天数分别为75,79,82,73,81.已知73对应的编号为145,75对应的编号是多少?并求这五个人加班天数的方差.
如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°,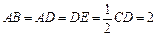 ,M是线段AE上的动点.
,M是线段AE上的动点.
(1)试确定点M的位置,使AC∥平面MDF,并说明理由;
(2)在(1)的条件下,求平面MDF将几何体ADE-BCF分成的两部分的体积之比.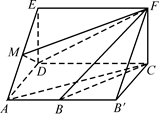
某城市随机抽取一年(365天)内100天的空气质量指数API的监测数据,结果统计如下:
| API |
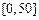 |
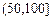 |
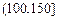 |
 |
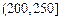 |
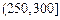 |
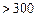 |
| 空气质量 |
优 |
良 |
轻微污染 |
轻度污染 |
中度污染 |
中度重污染 |
重度污染 |
| 天数 |
4 |
13 |
18 |
30 |
9 |
11 |
15 |
记某企业每天由空气污染造成的经济损失S(单位:元),空气质量指数API为ω。在区间[0,100]对企业没有造成经济损失;在区间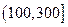 对企业造成经济损失成直线模型(当API为150时造成的 经济损失为500元,当API为200时,造成的经济损失为700元);当API大于300时造成的 经济损失为2000元;
对企业造成经济损失成直线模型(当API为150时造成的 经济损失为500元,当API为200时,造成的经济损失为700元);当API大于300时造成的 经济损失为2000元;
(1)试写出是S(ω)的表达式;
(2)试估计在本年内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;
(3)若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染,完成下面2×2列联表,并判断能否有95%的把握认为该市本年空气重度污染与供暖有关?
|
附: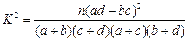
| 非重度污染 |
重度污染 |
合计 |
|
| 供暖季 |
|||
| 非供暖季 |
|||
| 合计 |
100 |
设 分别是椭圆
分别是椭圆 的 左,右焦点。
的 左,右焦点。
(1)若P是该椭圆上一个动点,求 的 最大值和最小值。
的 最大值和最小值。
(2)设过定点M(0,2)的 直线l与椭圆交于不同的两点A、B,且∠AOB为锐角(其中O为坐标原点),求直线l斜率k的取值范围。
已知函数f(x)=ex+2x2—3x
(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2) 当x ≥1时,若关于x的不等式f(x)≥ax恒成立,求实数a的取值范围;
(3)求证函数f(x)在区间[0,1)上存在唯一的极值点,并用二分法求函数取得极值时相应x的近似值(误差不超过0.2);(参考数据e≈2.7, ≈1.6,e0.3≈1.3)。
≈1.6,e0.3≈1.3)。
已知a,b均为正数,且a+b=1,证明:
(1)
(2)