(本小题满分12分)如图,两同心圆(圆心在原点)分别与 、
、 交于
交于 、
、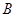 两点,其中
两点,其中 ,
, ,阴影部分为两同心圆构成的扇环,已知扇环的面积为
,阴影部分为两同心圆构成的扇环,已知扇环的面积为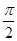 .
.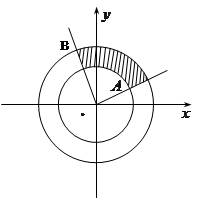
(Ⅰ)设角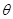 的始边为
的始边为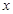 轴的正半轴,终边为
轴的正半轴,终边为 ,求
,求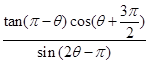 的值;
的值;
(Ⅱ)求点 的坐标.
的坐标.
已知数列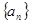 和
和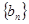 中,数列
中,数列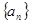 的前
的前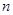 项和为
项和为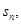 若点
若点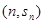 在函数
在函数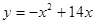 的图象上,点
的图象上,点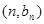 在函数
在函数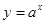 的图象上.设数列
的图象上.设数列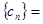
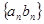 .
.
(Ⅰ)求数列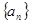 的通项公式;
的通项公式;
(Ⅱ)求数列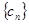 的前
的前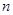 项和
项和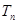 ;
;
(Ⅲ)求数列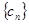 的最大值.
的最大值.
(本小题满分12分)设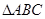 的内角
的内角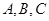 所对的边分别为
所对的边分别为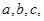 且
且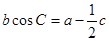 .
.
(Ⅰ)求角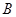 的大小;
的大小;
(Ⅱ)若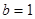 ,求
,求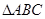 的周长
的周长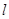 的取值范围.
的取值范围.
(本小题满分12分)已知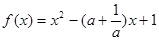 .
.
(Ⅰ)当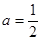 时,解不等式
时,解不等式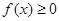 ;
;
(Ⅱ)若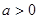 ,解关于x的不等式
,解关于x的不等式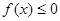 .
.
(本小题满分12分)某制造商3月生产了一批乒乓球,从中随机抽样100个进行检查,测得每个球的直径(单位:mm),将数据分组如下:
| 分组 |
频数 |
频率 |
| [39.95,39.97) |
10 |
|
| [39. 97,39.99) |
20 |
|
| [39.99,40.01) |
50 |
|
| [40.01,40.03] |
20 |
|
| 合计 |
100 |

(Ⅰ)请在上表中补充完成频率分布表(结果保留两位小数),并在图中画出频率分布直方图;
(Ⅱ)若以上述频率作为概率,已知标准乒乓球的直径为40.00 mm,试求这批球的直径误差不超过0.03 mm的概率;
(Ⅲ)统计方法中,同一组数据经常用该组区间的中点值(例如区间[39.99,40.01)的中点值是40.00作为代表.据此估计这批乒乓球直径的平均值(结果保留两位小数).
(本小题满分12分)设 的内角
的内角 所对应的边长分别是
所对应的边长分别是 且
且
(Ⅰ)当 时,求
时,求 的值;
的值;
(Ⅱ)当 的面积为3时,求
的面积为3时,求 的值.
的值.