(本小题12分)已知 的两边
的两边 的长是关于
的长是关于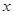 的一元二次方程
的一元二次方程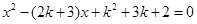 的两个实数根,第三边BC长为5.
的两个实数根,第三边BC长为5.
(1)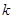 为何值时,
为何值时, 是以
是以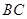 为斜边的直角三角形。
为斜边的直角三角形。
(2)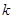 为何值时,
为何值时, 是等腰三角形,并求此时三角形的周长。
是等腰三角形,并求此时三角形的周长。
(本小题共12分) 在平面直角坐标系中,已知An(n,an)、Bn(n,bn)、Cn(n-1,0)(n∈N*),满足向量 与向量
与向量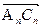 共线,且点An(n,an) (n∈N*)都在斜率为2的同一条直线l上. 若
共线,且点An(n,an) (n∈N*)都在斜率为2的同一条直线l上. 若 a1=-3,b1=10
a1=-3,b1=10 (1)求数列{an}与{ bn }的通项公式;
(1)求数列{an}与{ bn }的通项公式;
(2)求当n取何值时△AnBnCn的面积Sn最小,并求出Sn的这个最小值。
(本小题满分12分)
已知函数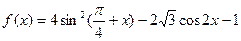 ,且
,且
(1)求 的最大值及最小值;(2)求
的最大值及最小值;(2)求 的在定义域上的单调区间.
的在定义域上的单调区间.
(本小题满分12分)椭圆C: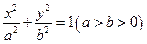 的两个焦点为
的两个焦点为 ,点P在椭圆C上,且
,点P在椭圆C上,且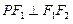 ,
, .(1)求椭圆C的方程;(2)若直线
.(1)求椭圆C的方程;(2)若直线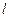 过圆
过圆 的圆心M,交椭圆C于A、B两点,且A、B两点关于点M对称,求直线
的圆心M,交椭圆C于A、B两点,且A、B两点关于点M对称,求直线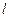 的方程。
的方程。
(本小题满分14分)已知动圆过定点F(2,0),且与直线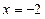 相切。(1)求动圆圆心的轨迹C的方程;(2)若经过定点F的动直线
相切。(1)求动圆圆心的轨迹C的方程;(2)若经过定点F的动直线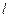 与轨迹C交于A、B两点,且这两点的横坐标分别为
与轨迹C交于A、B两点,且这两点的横坐标分别为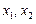 .①求证:
.①求证: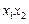 为定值;②试用
为定值;②试用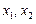 表示线段AB的长度;③求线段AB长度的最小值。
表示线段AB的长度;③求线段AB长度的最小值。
(本小题满分12分)在等差数列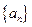 中,
中,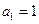 ,数列
,数列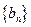 满足
满足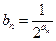 ,且
,且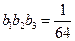 (1)求数列
(1)求数列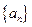 的通项公式;(2)求数列
的通项公式;(2)求数列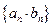 的前
的前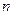 项的和
项的和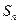 .
.