(本小题满分12分)椭圆C: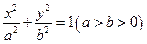 的两个焦点为
的两个焦点为 ,点P在椭圆C上,且
,点P在椭圆C上,且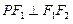 ,
, .(1)求椭圆C的方程;(2)若直线
.(1)求椭圆C的方程;(2)若直线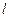 过圆
过圆 的圆心M,交椭圆C于A、B两点,且A、B两点关于点M对称,求直线
的圆心M,交椭圆C于A、B两点,且A、B两点关于点M对称,求直线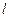 的方程。
的方程。
已知等差数列{an}的首项a1=1,公差d>0,且第2项、第5项、第14项分别为等比数列{bn}的第2项、第3项、第4项.
(1)求数列{an},{bn}的通项公式;
(2)设数列{cn}对n∈N*,均有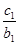 +
+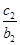 +…+
+…+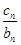 =an+1成立,求c1+c2+c3+…+c2014的值.
=an+1成立,求c1+c2+c3+…+c2014的值.
已知等差数列{an}中,a5=12,a20=-18.
(1)求数列{an}的通项公式;
(2)求数列{|an|}的前n项和Sn.
已知数列{an}的各项均为正数,前n项和为Sn,且满足2Sn= +n-4.
+n-4.
(1)求证{an}为等差数列;
(2)求{an}的通项公式.
设数列{an}的前n项和Sn满足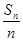 =3n-2.
=3n-2.
(1)求数列{an}的通项公式;
(2)设bn= ,Tn是数列{bn}的前n项和,求使得Tn<
,Tn是数列{bn}的前n项和,求使得Tn<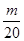 对所有n∈N*都成立的最小正整数m.
对所有n∈N*都成立的最小正整数m.
已知数列{an}的通项公式为an=n2-n-30.
(1)求数列的前三项,60是此数列的第几项?
(2)n为何值时,an=0,an>0,an<0?
(3)该数列前n项和Sn是否存在最值?说明理由.