(本小题满分12分)
已知函数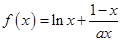 ,其中
,其中 .
.
(1)若函数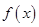 在区间
在区间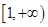 内单调递增,求
内单调递增,求 的取值范围;
的取值范围;
(2)求函数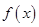 在区间
在区间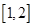 上的最小值;
上的最小值;
(3)求证:对于任意的 ,且
,且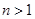 时,都有
时,都有 成立.
成立.
甲乙两人进行掰手腕比赛,比赛规则规定三分钟为一局,三分钟内不分胜负为平局,当有一人赢3局就结束比赛,否则继续进行,根据以往经验,每次甲胜的概率为 ,乙胜的概率为
,乙胜的概率为 ,且每局比赛胜负互不受影响.
,且每局比赛胜负互不受影响.
(Ⅰ)求比赛4局乙胜的概率;
(Ⅱ)求在2局比赛中甲的胜局数为ξ的分布列和数学期望;
(Ⅲ)若规定赢一局得2分,平一局得1分,输一局得0分,比赛进行五局,积分有超过5分者比赛结束,否则继续进行,求甲得7分的概率.
甲、乙两袋装有大小相同的红球和白球,甲袋装有2个红球,2个白球;乙袋装有2个红球,n个白球.现从甲,乙两袋中各任取2个球.
(Ⅰ)若n=3,求取到的4个球全是红球的概率;
(Ⅱ)若取到的4个球中至少有2个红球的概率为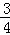 ,求n.
,求n.
已知p:方程x2+mx+1=0有两个不等的负实根,q:方程4x2+4(m﹣2)x+1=0无实根.若“p或q”为真,“p且q”为假.求实数m的取值范围.
五个人站成一排,求在下列条件下的不同排法种数:
(1)甲必须在排头;
(2)甲、乙相邻;
(3)甲不在排头,并且乙不在排尾;
(4)其中甲、乙两人自左向右从高到矮排列且互不相邻.
分别写出下列命题的逆命题、逆否命题,并判断它们的真假:
(1)若q<1,则方程x2+2x+q=0有实根;
(2)若x2+y2=0,则x,y全为零.