(本小题满分13分)在平面直角坐标系 中,椭圆
中,椭圆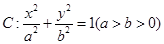 过点
过点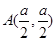 和点
和点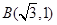 .
.
(1)求椭圆 的方程;
的方程;
(2)已知点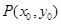 在椭圆
在椭圆 上,
上,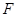 为椭圆的左焦点,直线
为椭圆的左焦点,直线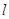 的方程为
的方程为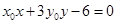 .
.
(i)求证:直线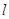 与椭圆
与椭圆 有唯一的公共点;
有唯一的公共点;
(ii)若点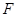 关于直线
关于直线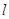 的对称点为
的对称点为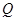 ,探索:当点
,探索:当点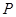 在椭圆
在椭圆 上运动时,直线
上运动时,直线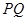 是否过定点?
是否过定点?
若过定点,求出此定点的坐标;若不过定点,请说明理由.
已知A、B为抛物线C:y2 = 4x上的两个动点,点A在第一象限,点B在第四象限l1、l2分别过点A、B且与抛物线C相切,P为l1、l2的交点.
(1)若直线AB过抛物线C的焦点F,求证:动点P在一条定直线上,并求此直线方程;
(2)设C、D为直线l1、l2与直线x = 4的交点,求 面积的最小值.
面积的最小值.
某地一渔场的水质受到了污染.渔场的工作人员对水质检测后,决定往水中投放一种药剂来净化水质. 已知每投放质量为 个单位的药剂后,经过x天该药剂在水中释放的浓度y(毫克/升)满足y=mf(x),其中
个单位的药剂后,经过x天该药剂在水中释放的浓度y(毫克/升)满足y=mf(x),其中 ,当药剂在水中释放的浓度不低于6(毫克/升)时称为有效净化;当药剂在水中释放的浓度不低于6(毫克/升)且不高于18(毫克/升)时称为最佳净化.
,当药剂在水中释放的浓度不低于6(毫克/升)时称为有效净化;当药剂在水中释放的浓度不低于6(毫克/升)且不高于18(毫克/升)时称为最佳净化.
(1)如果投放的药剂质量为m=6,试问渔场的水质达到有效净化一共可持续几天?
(2)如果投放的药剂质量为m,为了使在8天(从投放药剂算起包括第8天)之内的渔场的水质达到最佳净化,试确定应该投放的药剂质量m的取值范围.
某联欢晚会举行抽奖活动,举办方设置了甲、乙两种抽奖方案,方案甲的中奖率为 ,中奖可以获得2分;方案乙的中奖率为
,中奖可以获得2分;方案乙的中奖率为 ,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.
,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.
(1)张三选择方案甲抽奖,李四选择方案乙抽奖,记他们的累计得分为X,若X≤3的概率为 ,求
,求 ;
;
(2)若张三、李四两人都选择方案甲或都选择方案乙进行抽奖,问:他们选择何种方案抽奖,累计得分的数学期望较大?
在如图所示的几何体中, 平面
平面 ,
, ∥
∥ ,
, 是
是 的中点,
的中点, ,
, .
.
(1)证明: ∥平面
∥平面 ;
;
(2)求二面角 的大小的余弦值.
的大小的余弦值.
已知函数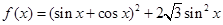 .
.
(1)求函数f (x)的最小正周期;
(2)在△ABC中,角A,B,C的对边分别是a,b,c,且满足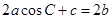 ,求f(B)的取值范围.
,求f(B)的取值范围.