如图，分别以菱形BCED的对角线BE、CD所在直线为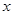
轴、
轴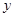建立平面直角坐标系，抛物线
（
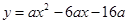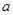＜0）过B、C两点，与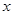轴的负半轴交于点A，且∠ACB=90°．点P是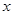轴上一动点，设点P的坐标为（
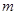，0），过点P作直线
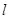垂直于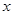轴，交抛物线于点Q．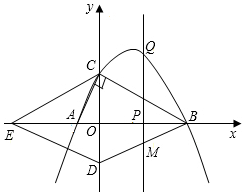
（1）求点A、B、C的坐标及抛物线的解析式；
（2）当点P在线段OB上运动时，直线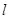交BD于点M，试探究：
①求MQ的大小；（用含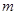的化简式子表示）
②当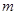为何值时，四边形CQBM的面积取得最大值，并求出这个最大值．
（3）当点P在线段EB上运动时，是否存在点 Q，使△BDQ为直角三角形，若存在，请直接写出点Q的坐标；若不存在，请说明理由
：
，过点
的直线
交抛物线
，
两点．
，求该抛物线的方程；
，
，交于点
，以线段
为直径的圆经过点
的值．
，其中
且
．
时，若
无解，求
的范围；
，
（
），使得
时，函数
的值域都也为
，求
的前
项和为
，已知
，
，
．
，求证：数列
是等比数列；
的取值范围．
中，
平面
，底面
，
，
且
为
的中点．
平面
；
与平面
所成角的正切值．
，
，函数
．
的最小正周期；
在
上的值域．