(本小题满分12分)
已知函数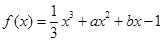 的导函数
的导函数 为偶函数,直线
为偶函数,直线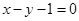 是
是 的一条切线.(1).求
的一条切线.(1).求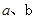 的值 (2).若
的值 (2).若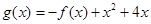 ,求
,求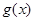 的极值.
的极值.
(本小题满分13分)
已知向量 ,
,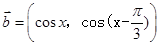 ,函数
,函数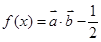 .
.
(1)求函数 的最小正周期;
的最小正周期;
(2)若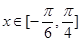 时,求
时,求 的值域.
的值域.
本小题满分13分)
某学校在一次庆祝活动中组织了一场知识竞赛,该竞赛设有三轮,前两轮各有四题,只有答
正确其中三题,才能进入下一轮,否则将被淘汰。最后第三轮有三题,这三题都答对的同学
获得奖金500元.某同学参与了此次知识竞赛,且该同学前两轮每题答正确的概率均为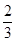 ,
,
第三轮每题答正确的概率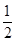 ,各题正确与否互不影响.在竞赛过程中,该同学不放弃所有机
,各题正确与否互不影响.在竞赛过程中,该同学不放弃所有机
会.
(1)求该同学能进入第三轮的概率;
(2)求该同学获得500元奖金的概率.
(本小题满分13分)
已知等差数列 中,
中,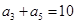 ,
, 的前
的前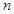 项和为
项和为 ,
,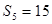 .
.
(1).求数列 的通
的通 项公式
项公式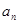 ;
;
(2).设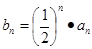 ,求数列
,求数列 的前
的前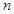 和
和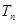 .
.
(本小题满分12分,( 1)小问6分,(2)小分6分.)
1)小问6分,(2)小分6分.)
已知函数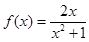 ,数列
,数列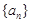 满足
满足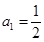 ,
,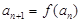 ,
,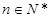 .
.
(1)求证: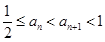 ;
;
(2)求证: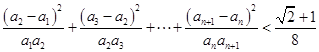 .
.