(本小题满分16分)已知数列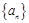 的前
的前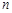 项和
项和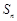 满足:
满足: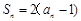 ,数列
,数列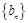 满足:对任意
满足:对任意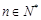 有
有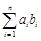
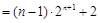 .
.
(1)求数列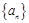 与数列
与数列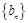 的通项公式;
的通项公式;
(2)记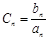 ,数列
,数列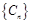 的前
的前 项和为
项和为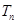 ,证明:当
,证明:当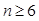 时,
时,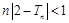 .
.
(本小题满分12分)
已知数列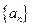 是等差数列,
是等差数列,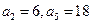 ;数列
;数列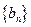 的
的 前n项和是
前n项和是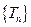 ,且
,且 .
.
(Ⅰ) 求数列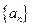 的通项公式;
的通项公式;
(Ⅱ) 求证:数列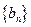 是等比数列;
是等比数列;
(Ⅲ) 记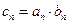 ,求
,求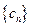 的前n项和
的前n项和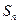 .
.
(本小题满分12分)
已知 .
.
(Ⅰ)若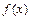 在
在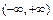 上为增函数,求实数a的取值范围;
上为增函数,求实数a的取值范围;
(Ⅱ)当常数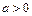 时,设
时,设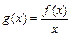 ,求
,求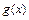 在
在 上的最大值和最小值.
上的最大值和最小值.
(本小题满分12分)
在四边形ABCD中,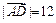 ,
,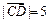 ,
,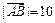 ,
,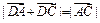 ,
,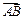 在
在 方向上的投影为8;
方向上的投影为8;
(1)求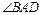 的正弦值;(2)求
的正弦值;(2)求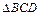 的面积.
的面积.
(本小题满分12分)
数列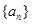 中,
中,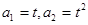 ,其中
,其中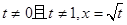 是函数
是函数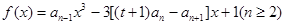 的一个极值点。
的一个极值点。
(1)证明 :数列
:数列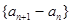 是等比数列;
是等比数列;
(2)求
(本小题满分12分)
设函数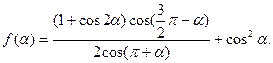
(I)设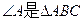 的内角,且为钝角,求
的内角,且为钝角,求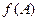 的最小值;
的最小值;
(II)设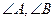 是锐角
是锐角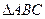 的内角,且
的内角,且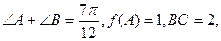 求
求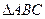 的三个内角的大小和AC边的
的三个内角的大小和AC边的 长。
长。