某公司从大学招收毕业生，经过综合测试，录用了14名男生和6名女生，这20名毕业生的测试成绩如茎叶图所示（单位：分）．公司规定：成绩在180分以上者到甲部门工作，180分以下者到乙部门工作，另外只有成绩高于180分的男生才能担任助理工作．
（1）如果用分层抽样的方法从甲部门人选和乙部门人选中选取8人，再从这8人中选3人，那么至少有一人是甲部门人选的概率是多少？
（2）若从所有甲部门人选中随机选3人，用X表示所选人员中能担任助理工作的人数，写出X的分布列，并求出X的数学期望．
已知集合
，集合
，集合
，
（Ⅰ）求
； （Ⅱ）若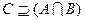
，试确定实数
的取值范围.
已知命题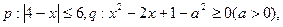
若非
是
的充分不
必要条件，求
的取值范围。
已知x与y之间的一组数据
| x |
0 |
1 |
2 |
3 |
| y |
1 |
3 |
5 |
7 |
(1)画出散点图
（2）若
x与y线性相关，写出线性回归方程必定经过的点
（3）若x与y线性相关求出线性回归方程，
（4）说出2个刻画回归效果的手段，假设R
=0.74
说明什么问题。
参考公式
（本小题满分12分）
设z1=1+2ai，z2=a-i（a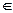
R），已知A={z||z-z1|≤1}，B={z||z-z2|≤2}，A∩B=φ，求a的取值范围
（本小题满分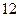
分）有甲、乙两个班，进行数学考试，按学生考试及格与不及格统计成绩后，得到如下的列联表
| 不及格 |
及格 |
总计 |
|
| 甲班 |
10 |
35 |
M |
| 乙班 |
7 |
38 |
45 |
| 总计 |
17 |
73 |
N |
（1）求M,N的值
（2）写出求k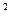
观测值的计算式
（3）假设k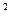=0.6527你有多大把握认为成绩及格与班级
有关？
k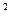=7.121又说明什么？
（P（k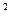
）
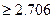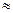0.100，P（k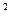
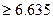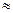）0.010）