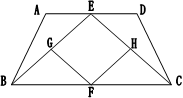
如图,大海中有A和B两个岛屿,为测量它们之间的距离,在海岸线PQ上点E处测得∠AEP=74°,∠BEQ=30°;在点F处测得∠AFP=60°,∠BFQ=60°,EF=1km.
(1)判断AB,AE的数量关系,并说明理由;
(2)求两个岛屿A和B之间的距离(结果精确到0.1km).
(参考数据: ≈1.73,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49,sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
≈1.73,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49,sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
小明家今年种植的“红灯”樱桃喜获丰收,采摘上市20天全部销售完,小明对销售情况进行了跟踪记录,并将记录情况绘成图象,日销售量y(单位:千克)与上市时间x(单位:天)的函数关系如图1所示,樱桃价格z(单位:元/千克)与上市时间x(单位:天)的函数关系如图2所示。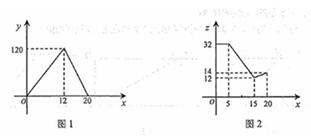
(1)观察图象,直接写出日销售量的最大值;
(2)求李明家樱桃的日销售量y与上市时间x的函数解析式;
(3)试比较第10天与第12天的销售金额哪天多?
为了从甲、乙两名同学中选拔一个参加射击比赛,对他们的射击水平进行了测验,两个在相同条件下各射靶10次,命中的环数如下(单位:环):
甲:7,8,6,8,6,5,9,10,7,4
乙:9,5,7,8,6,8,7,6,7,7
求 ,
,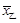 ,
,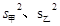 ;你认为该选拔哪名同学参加射击比赛?
;你认为该选拔哪名同学参加射击比赛?
已知:矩形ABCD中,对角线AC与BD交与点O,∠BOC=120°,AC=4cm.求:矩形ABCD的周长和面积。
如图,在△ABC中,AD⊥BC,垂足为D,∠B=60°,∠C=45°.
(1)求∠BAC的度数.
(2)若AC=2,求AD的长.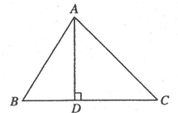
如图,已知:等腰梯形ABCD中,AD∥BC,AB=CD,E、F、G、H分别是AD、BC、BE、CE的中点
(1)求证:△ABE≌△DCE
(2)四边形EGFH是什么特殊四边形?并证明你的结论.
(3)连接EF,当四边形EGFH是正方形时,线段EF与GH有什么数量关系?请说明理由.