（本小题满分12分）已知椭圆
＞
＞
的离心率为
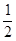，以坐标原点为圆心，椭圆的短半轴长为半径的圆与直线
相切。
（1）求椭圆C的标准方程；
（2）设点
，
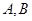是椭圆C上关于
轴对称的任意两个不同的点，连结
交椭圆
于另一点
，证明：直线
与轴相交于定点．
设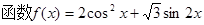
（1）求函数
的最小正周期和单调递
增区间
(2)当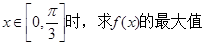
(14分)设圆满足：①截y轴所得弦长为2；②被x轴分成两段圆弧，其弧长的比为3∶1，在满足条件①、②的所有圆中，求圆心到直线l:x-2y=0的距离最小的圆的方程。
(12分)已知曲线C：x2+y2-2x-4y+m=0
（1）当m为何值时，曲线C表示圆；
（2）若曲线C与直线x+2y-4=0交于M、N两点，且OM⊥ON(O为坐标原点)，求m的值。
(12分)自点A(-3，3)发出的光线L射到x轴上，被x轴反射，其反射光线所在直线与圆x2+y2-4x-4y+7=0相切，求光线L所在直线的方程。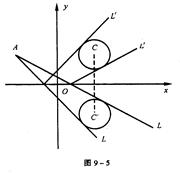
(12分)如图7-4，已知△ABC中， ∠ACB=90°，CD⊥AB，且AD=1，BD=2，△ACD绕CD旋转至A′CD，使点A′与点B之间的距离A′B=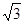
。
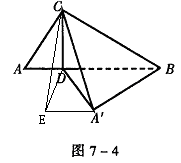
（1）求证：BA′⊥平面A′CD；
（2）求二面角A′－CD－B的大小；
（3）求异面直线A′C与BD所成的角的余弦值。