(14分)设圆满足:①截y轴所得弦长为2;②被x轴分成两段圆弧,其弧长的比为3∶1,在满足条件①、②的所有圆中,求圆心到直线l:x-2y=0的距离最小的圆的方程。
(本小题满分14分)
过 轴上动点
轴上动点 引抛物线
引抛物线
 的两条切线
的两条切线 、
、 ,
,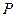 、
、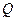 为切点,设切线
为切点,设切线 ,
, 的斜率分别为
的斜率分别为 和
和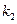 .
.
(1)求证: ;
;
(2)试问:直线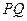 是否经过定点?若是,求出该定点坐标;若不是,请说明理由.
是否经过定点?若是,求出该定点坐标;若不是,请说明理由.
.(本小题满分12分)
如图,已知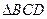 中,
中, ,
, 平面
平面 ,
,
 分别为
分别为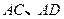 的中点.
的中点.
(1)求证:平面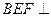 平面
平面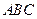 ;
;
(2)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
(本小题满分12分)
已知曲线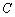 的极坐标方程是
的极坐标方程是 ,直线
,直线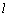 的参数方程是
的参数方程是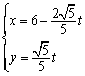
(1)求曲线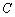 和直线
和直线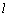 的直角坐标方程;
的直角坐标方程;
(2)设点 为曲线
为曲线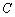 上任一点,求
上任一点,求 到直线
到直线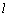 的距离的最大值.
的距离的最大值.
已知圆 :
: 与
与 轴交于点
轴交于点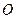 、
、
 ,与
,与 轴交于点
轴交于点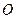 、
、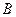 ,其中
,其中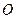 为原点.
为原点.
函数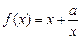 (
(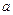 为常数)的图象过点
为常数)的图象过点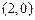 ,
,
(Ⅰ)求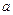 的值并判断
的值并判断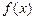 的奇偶性;
的奇偶性;
(Ⅱ)函数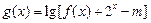 在区间
在区间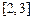 上
上 有意义,求实数
有意义,求实数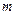 的取值范围;
的取值范围;
(Ⅲ)讨论关于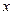 的方程
的方程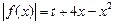
 (
(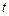 为常数)的正根的个数.
为常数)的正根的个数.