函数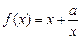 (
(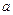 为常数)的图象过点
为常数)的图象过点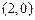 ,
,
(Ⅰ)求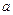 的值并判断
的值并判断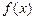 的奇偶性;
的奇偶性;
(Ⅱ)函数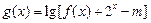 在区间
在区间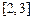 上
上 有意义,求实数
有意义,求实数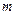 的取值范围;
的取值范围;
(Ⅲ)讨论关于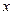 的方程
的方程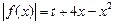
 (
(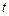 为常数)的正根的个数.
为常数)的正根的个数.
设函数f(x)=x2-(a-2)x-alnx.
(1)求函数f(x)的单调区间;
(2)若函数f(x)有两个零点,求满足条件的最小正整数a的值;
(3)若方程f(x)=c有两个不相等的实数根x1、x2,求证:f′ >0.
>0.
已知函数f(x)=lnx-ax(a∈R).
(1)求函数f(x)的单调区间;
(2)当a>0时,求函数f(x)在[1,2]上的最小值.
某地方政府在某地建一座桥,两端的桥墩相距m米,此工程只需建两端桥墩之间的桥面和桥墩(包括两端的桥墩).经预测,一个桥墩的费用为256万元,相邻两个桥墩之间的距离均为x,且相邻两个桥墩之间的桥面工程费用为(1+ )x万元,假设所有桥墩都视为点且不考虑其他因素,记工程总费用为y万元.
)x万元,假设所有桥墩都视为点且不考虑其他因素,记工程总费用为y万元.
(1)试写出y关于x的函数关系式;
(2)当m=1280米时,需要新建多少个桥墩才能使y最小?
请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A、B、C、D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE=FB=xcm.
(1)某广告商要求包装盒侧面积S(cm2)最大,试问x应取何值?
(2)某厂商要求包装盒容积V(cm3)最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值.
已知函数f(x)=ax3+bx2-3x(a、b∈R)在点x=-1处取得极大值为2.
(1)求函数f(x)的解析式;
(2)若对于区间[-2,2]上任意两个自变量的值x1、x2,都有|f(x1)-f(x2)|≤c,求实数c的最小值.