(本小题满分14分)如图,平面PAC⊥平面ABC,点E、F、O分别为线段PA、PB、AC的中点,点G是线段CO的中点,AB=BC=AC=4,PA=PC=2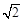 .求证:
.求证:
(1)PA⊥平面EBO;
(2)FG∥平面EBO.
已知函数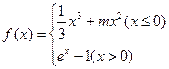
(1)讨论函数f (x)的极值情况;
(2)设g (x) =" ln" (x + 1),当x1>x2>0时,试比较f (x1 – x2)与g (x1 – x2)及g (x1) –g (x2)三者的大小;并说明理由.(参考公式: 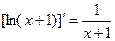 )
)
已知点P (4,4),圆C: 与椭圆E:
与椭圆E: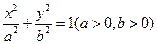 的一个公共点为A(3,1),F1,F2分别是椭圆的左、右焦点,直线
的一个公共点为A(3,1),F1,F2分别是椭圆的左、右焦点,直线 与圆C相切。
与圆C相切。
(1)求m的值与椭圆E的方程;
(2)设D为直线PF1与圆C 的切点,在椭圆E上是否存在点Q ,使△PDQ是以PD为底的等腰三角形?若存在,请指出共有几个这样的点?并说明理由。
 、
、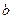 是常数,关于
是常数,关于 的一元二次方程
的一元二次方程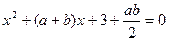 有实数解记为
有实数解记为
事件A.
(1)若 、
、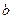 分别表示投掷两枚均匀骰子出现的点数,求
分别表示投掷两枚均匀骰子出现的点数,求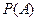 ;
;
(2)若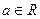 、
、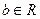 ,
, 且
且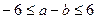 ,求
,求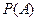
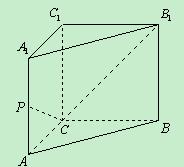
如图,在直三棱柱 中,
中, ,
, .
.
(1) 下图给出了该直三棱柱三视图中的主视图,请据此画出它的左视图和俯视图;
(2) 若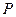 是
是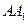 的中点,求四棱锥
的中点,求四棱锥 的体积.
的体积.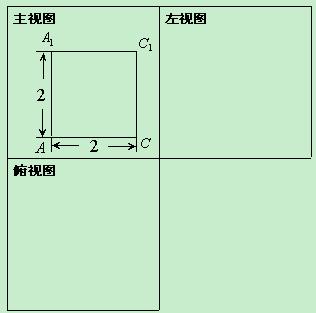
已知:A、B、C是 的内角,
的内角, 分别是其对边长,向量
分别是其对边长,向量 ,
,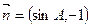 ,
,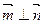 .(Ⅰ)求角A的大小;(Ⅱ)若
.(Ⅰ)求角A的大小;(Ⅱ)若 求
求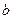 的长
的长