如图所示，一绝热气缸倒立竖放在两水平台面上，缸内一光滑活塞密封了一定质量的理想气体。在活塞下挂有一物块，活塞与物块的总重力G="30" N，活塞的横截面积S=3.0×l0-3m2。活塞静止时，缸内气体温度t1=27oC，体积V1=3.0×l0-3m3，外界的大气压强恒为p0= 1.0×105Pa。缸内有一个电阻丝，电阻丝的电阻值恒为R=5.0Ω,电源电动势E="18" V、内阻r="1.0" Ω。闭合开关20 s后，活塞缓慢下降高度h="0.10" m，求这20 s内气体内能的变化量和20 s末缸内气体的温度。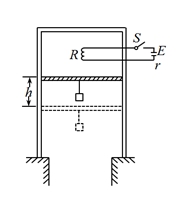
有一个直流电动机，把它接入0.2V电压的电路时，电机不转，此时测得流过电动机的电流是0.4A；若把电动机接入2.0V电压的电路中，电动机正常工作，工作电流是1.0A。求：
（1）电动机线圈的电阻；
（2）电动机正常工作时的输出功率；
（3）在发动机正常工作时，转子突然被卡住，此时电动机的发热功率。
如图所示，倾角为θ的光滑斜面上有一根水平方向的通电直导线恰好静止。已知直导线长为l，质量为m，电流方向垂直于纸面向外，电流强度为I，整个装置处在匀强磁场中。则
（1）匀强磁场的磁感强度的最小值B1的大小和方向是怎样的？
（2）要使静止在斜面上的通电直导线对斜面无压力，匀强磁场的磁感强度的最小值B2的大小和方向是怎样的？
如图所示，平行板电容器竖直放置在水平绝缘地板上，一个带电质点质量为m=0.10×10- 3kg，电荷量为q=" -" 2.0×10- 4C，从电容器中心线上某点由静止开始自由下落，下落了h1=0.80m后进入匀强电场，又下落了h2=1.0m后到达水平绝缘地板。落地点在两板中心O点左侧s=20cm处（未碰板）。g取10m/s2。求：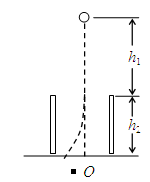
（1）带电质点在空中运动的时间；
（2）电容器中匀强电场的场强E的大小和方向。
为了研究过山车的原理，物理小组提出了下列的设想：取一个与水平方向夹角为37°、长为L=2.0m的粗糙的倾斜轨道AB，通过水平轨道BC与竖直圆轨道相连，出口为水平轨道DE，整个轨道除AB段以外都是光滑的。其中AB与BC轨道以微小圆弧相接，如图所示。一个质量为2kg的小物块以初速度v0＝4.0m/s，从某一高处水平抛出，恰从A点无碰撞地沿倾斜轨道滑下。已知物块与倾斜轨道AB的动摩擦因数μ＝0.5（g取10m/s2，sin37°＝0.6，cos37°＝0.8）：
（1）求小物块的抛出点和A点的高度差；
（2）求小物块沿着轨道AB运动的过程中克服摩擦力所做的功；
（3）为了让小物块能沿着轨道运动，并从E点飞出，则竖直圆轨道的半径应该满足什么条件?
一水平的浅色长传送带上放置一煤块（可视为质点），煤块与传送带之间的动摩擦因数为
。初始时，传送带与煤块都是静止的。现让传送带以恒定的加速度a0开始运动,当其速度达到v0后，便以此速度做匀速运动。经过一段时间，煤块在传送带上留下了一段黑色痕迹后，煤块相对于传送带不再滑动。求:
（1）传送带从静止开始加速到v0所需的时间；
（2）从传送带开始运动到速度刚达到v0这段时间内，煤块相对地面的位移大小；
（3）煤块在传送带上留下黑色痕迹的长度。