如图,在△ABC中,点D是BC的中点,点F是AD的中点,过点D作DE∥AC,交CF的延长线于点E,连接BE,AE.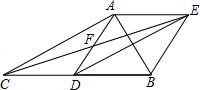
(1)求证:四边形ACDE是平行四边形;
(2)若AB=AC,试判断四边形ADBE的形状,并证明你的结论.
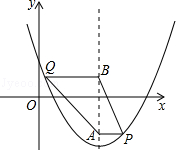
如图,在平面直角坐标系中,抛物线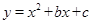 经过点(1,﹣1),且对称轴为在线
经过点(1,﹣1),且对称轴为在线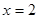 ,点P、Q均在抛物线上,点P位于对称轴右侧,点Q位于对称轴左侧,PA垂直对称轴于点A,QB垂直对称轴于点B,且QB=PA+1,设点P的横坐标为
,点P、Q均在抛物线上,点P位于对称轴右侧,点Q位于对称轴左侧,PA垂直对称轴于点A,QB垂直对称轴于点B,且QB=PA+1,设点P的横坐标为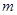 .
.
(1)求这条抛物线所对应的函数关系式;
(2)求点Q的坐标(用含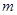 的式子表示);
的式子表示);
(3)请探究PA+QB=AB是否成立,并说明理由;
(4)抛物线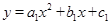 (
(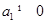 )经过Q、B、P三点,若其对称轴把四边形PAQB分成面积为1:5的两部分,直接写出此时
)经过Q、B、P三点,若其对称轴把四边形PAQB分成面积为1:5的两部分,直接写出此时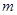 的值.
的值.
如图,在△ABC中,BA=BC,以AB为直径作⊙O,交AC于点D,连接DB,过点D作DE⊥BC,垂足为E.
(1)求证:DE为⊙O的切线;
(2)若DB=8,DE=2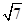 ,求⊙O半径的长.
,求⊙O半径的长.
如图,顶点为P(4,-4)的二次函数图象经过原点(0,0),点A在该图象上,OA交其对称轴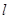 于点M,点M、N关于点P对称,连接AN、ON
于点M,点M、N关于点P对称,连接AN、ON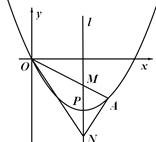
(1)求该二次函数的关系式.
(2)若点A的坐标是(6,-3),求△ANO的面积.
某养殖户每年的养殖成本包括固定成本和可变成本,其中固定成本每年均为4万元,可变成本逐年增长,已知该养殖户第1年的可变成本为2.6万元,设可变成本平均的每年增长的百分率为x.
(1)用含x的代数式表示第3年的可变成本为万元.
(2)如果该养殖户第3年的养殖成本为7.146万元,求可变成本平均每年增长的百分率x.
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB.
(1)求∠CAD的度数;
(2)延长AC至E,使CE=AC,求证:DA=DE.