如图,在平四边形ABCD中,对角线AC与BD相交于点O,P为线段BC上一点(除端点外),连接PO并延长交AD于点Q,延长BC到点E,使CE=BC,连接DE.
(1)求证:BP=DQ;
(2)已知AB=5,AC=6,若CD= BE,求△BDE的周长.
BE,求△BDE的周长.
“十一”黄金周期间,井冈山红色旅游在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
| 日期 |
1日 |
2日 |
3日 |
4日 |
5日 |
6日 |
7日 |
| 人数变化 单位:万人 |
+1.2 |
+0.8 |
+0.6 |
-0.4 |
-0.6 |
+0.2 |
-1.2 |
(1)、若9月30日的游客人数记为a,请用a的代数式表示10月2日的游客_________万人。
(2)、请判断七天内游客人数最多的是_______日;最少的是______日。它们相差___________万人?
(3)、以9月30日的游客人数为0点,用折线统计图表示这7天的游客人数情况:
人数变化(万人)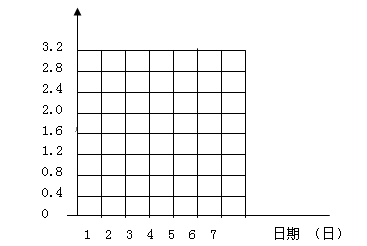
由一些大小相同的小正方体组成的简单几何体的主视图和俯视图如图:
(1)请你画出这个几何体的其中两种左视图;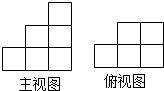
(2)若组成这个几何体的小正方体的块数为n,请你写出n的所有可能值.
某电信公司给顾客提供了两种手机上网计费方式,
方式A:以每分钟0.1元的价格按上网时间计费;
方式B:初收月基费20元外,再以每分钟0.06元的价格按上网时间计费;
假设顾客甲一个月手机上网的时间共有x 分钟,
⑴分别写出顾客甲按A、B两种方式计费的上网费用(用含x的代数式表示)
⑵若顾客甲一个月手机上网的时间共有250分钟,则他选择哪种方式合算?试说明理由。
(3)顾客甲一个月手机上网的时间共有多少分钟,他选择两种方式费用一样?
为了确保祖国母亲六十二华诞期间的用电安全,电力工人开车沿着一条南北方向的公路来回的行使,某一天早晨从A地出发,晚上到达了B地,约定向北为正,向南为负,当天记录如下(单位:千米):-17,+8,+6,-14,-8,+17,+5,-6
(1)问B地在A地何处,相距多少千米?
(2)若汽车行使每千米耗油0.2升,那么这一天共耗油多少升?
先化简,后求值: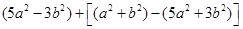 其中a=-1,b=1
其中a=-1,b=1