已知一条曲线C在y轴右边,C上每一点到点 的距离减去它到y轴距离的差都是
的距离减去它到y轴距离的差都是 .点A,B在曲线C上且位于x轴的两侧,
.点A,B在曲线C上且位于x轴的两侧,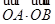 =2(其中O为坐标原点).
=2(其中O为坐标原点).
(Ⅰ)求曲线C的方程;
(Ⅱ)证明:直线AB恒过定点.
如图1,在直角梯形ABCD中, ,
, ,
, ,
, ,将
,将 沿
沿 折起,使平面
折起,使平面
 平面
平面 ,得到三棱锥
,得到三棱锥 ,如图2所示.
,如图2所示.

(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求点 到平面
到平面 的距离.
的距离.
设等差数列{an}的公差为d,点(an,bn)在函数f (x)=2x的图象上(n∈N*).
(Ⅰ)证明:数列{bn}为等比数列;
(Ⅱ)若a1=1,直线y=( ln2)(x-a2)+
ln2)(x-a2)+ 在x轴上的截距为2-
在x轴上的截距为2- ,求数列{anb
,求数列{anb }的前n项和Sn.
}的前n项和Sn.
设 的内角
的内角 所对的边长分别为
所对的边长分别为 ,且
,且 ,
, .
.
(Ⅰ)求 及边长
及边长 的值;
的值;
(Ⅱ)若 的面积
的面积 ,求
,求 的周长
的周长 .
.
已知抛物线 与双曲线
与双曲线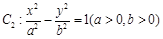 有公共焦点
有公共焦点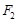 ,点
,点 是曲线
是曲线 在第一象限的交点,且
在第一象限的交点,且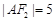 .
.
(Ⅰ)求双曲线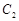 的方程;
的方程;
(Ⅱ)以双曲线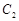 的另一焦点
的另一焦点 为圆心的圆
为圆心的圆 与直线
与直线 相切,圆
相切,圆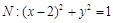 .过点
.过点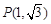 作互相垂直且分别与圆
作互相垂直且分别与圆 、圆
、圆 相交的直线
相交的直线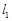 和
和 ,设
,设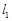 被圆
被圆 截得的弦长为
截得的弦长为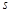 ,
, 被圆
被圆 截得的弦长为
截得的弦长为 ,问:
,问: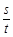 是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
是否为定值?如果是,请求出这个定值;如果不是,请说明理由.