下列四个命题:
①样本方差反映的是所有样本数据与样本平均值的偏离程度;
②某只股票经历了10个跌停(下跌10%)后需再经过10个涨停(上涨10%)就可以回到原来的净值;
③某校高三一级部和二级部的人数分别是m、n,本次期末考试两级部数学平均分分别是a、b,则这两个级部的数学平均分为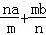 ;
;
④某中学采用系统抽样方法,从该校高一年级全体800名学生中抽50名学生做牙齿健康检查,现将800名学生从l到800进行编号.已知从497~513这16个数中取得的学生编号是503,则初始在第1小组1~16中随机抽到的学生编号是7.
其中真命题的个数是( )
| A.0个 | B.1个 | C.2个 | D.3个 |
设函数f(x)满足x2f′(x)+2xf(x)=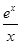 ,f(2)=
,f(2)=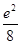 ,则x>0时,f(x)( ).
,则x>0时,f(x)( ).
| A.有极大值,无极小值 |
| B.有极小值,无极大值 |
| C.既有极大值又有极小值 |
| D.既无极大值也无极小值 |
已知f(x)是定义在(0,+∞) 上的非负可导函数,且满足xf′(x)+f(x)≤0,对任意的0<a<b,则必有( ).
| A.af(b)≤bf(a) | B.bf(a)≤af(b) |
| C.af(a)≤f(b) | D.bf(b)≤f(a) |
函数f(x)的定义域是R,f(0)=2,对任意x∈R,f(x)+f′(x)>1,则不等式ex·f(x)>ex+1的解集为( ).
A. |
B. |
C. |
D. |
下面四个图象中,有一个是函数f(x)= x3+ax2+(a2-1)x+1(a∈R)的导函数y=f′(x)图象,则f(-1)等于( ).
x3+ax2+(a2-1)x+1(a∈R)的导函数y=f′(x)图象,则f(-1)等于( ).
A. |
B.- |
C.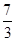 |
D.- 或 或 |
已知函数f(x)=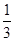 x3-2x2+3m,x∈[0,+∞),若f(x)+5≥0恒成立,则实数m的取值范围是( )
x3-2x2+3m,x∈[0,+∞),若f(x)+5≥0恒成立,则实数m的取值范围是( )
A.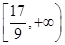 |
B.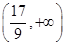 |
| C.(-∞,2] | D.(-∞,2) |