原命题为“三角形ABC中,若cosA <0,则三角形ABC为钝角三角形”,关于其逆命题,否命题,逆否命题真假性的判断依次如下,正确的是( )
| A.真,真,真 | B.假,假,真 |
| C.真,真,假 | D.真,假,假 |
若x,y满足 , 则
, 则 的最小值为()
的最小值为()
| A.4 | B.5 | C.6 | D.7 |
投掷一枚质地均匀的骰子两次,若第一次面向上的点数小于第二次面向上的点数,我们称其为正实验;若第二次面向上的点数小于第一次面向上的点数,我们称其为负实验;若两次面向上的点数相等,我们称其为无效.那么一个人投掷该骰子两次后出现无效的概率是()
A.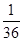 |
B.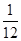 |
C.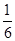 |
D.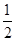 |
在一次实验中,测得 的四组值分别是
的四组值分别是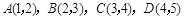 ,则
,则 与
与 之间的回归
之间的回归
直线方程为()
A.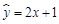 |
B. |
C.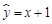 |
D.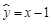 |
在 中,
中, 则
则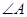 等于()
等于()
| A.60° | B.45° | C.120° | D.150° |
已知命题 ;命题
;命题 .则下列结论正确的是()
.则下列结论正确的是()
A.命题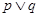 是假命题 是假命题 |
B.命题 是真命题 是真命题 |
C.命题 是真命题 是真命题 |
D.命题 是真命题 是真命题 |